F1_DG_Aula 05 – MRU: Velocidade Relativa

Na Aula 01 foi visto que para sabermos se um corpo está em movimento ou repouso, primeiro precisamos definir um referencial.

Portanto, não existe o conceito de velocidade absoluta, a qual seria independente de qualquer referencial e sim velocidades relativas, as quais sempre dependem de um dado sistema de referência.

Com base nessa informação, podemos definir “velocidade relativa entre corpos”, facilitando assim a resolução de muitos problemas em Física.

Obs.: como neste momento estamos estudando o movimento uniforme, onde a velocidade é constante, a velocidade relativa entre dois corpos também será constante e consequentemente a velocidade relativa coincide com a velocidade relativa média.

Matematicamente, podemos expressar por:

$\dpi{100} \mathbf{v_{rel}=v_{m}=\frac{\Delta s_{rel}}{\Delta t_{rel}}}$

Voltando a velocidade relativa entre corpos, para facilitar a aprendizagem, vamos dividir o assunto em três partes.

1 – Dois corpos se movimentando no mesmo sentido

É o caso das ultrapassagens durante uma viagem de carro.

Por exemplo, considere que você esteja viajando num carro que está a 100 km/h fazendo uma ultrapassagem por um caminhão que está a 90 km/h. Durante a ultrapassagem, apesar do velocímetro marcar 100 km/h, ao olhar para o caminhão você observa que está passando por ele muito lentamente.

Neste caso a velocidade relativa entre os corpos é igual à subtração, em módulo, das velocidades de cada um.

A expressão matemática que representa a velocidade relativa neste caso é definida como:

$\dpi{100} \mathbf{v_{rel.}=\left | v_{A} \right |+\left | v_{B} \right |}$

No nosso exemplo, a velocidade relativa entre o carro e o caminhão é de 10 km/h.

Lembrete: as duas barrinhas | | representam o módulo ou valor absoluto da grandeza em estudo.

Exemplo: $\dpi{100} \inline \mathbf{\left | +80 \right |=\left | -80 \right |=80}$

2 – Dois corpos se movimentando em sentidos opostos

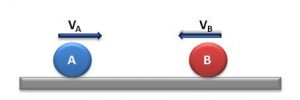
É o caso das passagens por outros carros que vem em sentido contrário ao seu durante uma viagem de carro por uma rodovia de mão dupla.

Por exemplo, considere que você esteja viajando num carro que está a 100 km/h e passa um caminhão que está vindo a 90 km/h. Durante a passagem, apesar do velocímetro marcar 100 km/h, ao olhar para o caminhão você observa que está passando por ele muito rapidamente.

Neste caso a velocidade relativa entre os corpos é igual a soma, em módulo, das velocidades de cada um.

A expressão matemática que representa a velocidade relativa neste caso é definida como:

$\dpi{100} \mathbf{v_{rel.}=\left | v_{A} \right |-\left | v_{B} \right |}$

No nosso exemplo, a velocidade relativa entre o carro e o caminhão é de 190 km/h.

3 – Um corpo em movimento e outro em repouso

É claro que nesse caso particular, a velocidade relativa é igual, em módulo, a velocidade do corpo que está em movimento.

No nosso exemplo: $\dpi{100} \inline \mathbf{v_{rel.}=\left | v_{A} \right |}$

Curiosidades

Você tem ideia da velocidade média de um projétil disparado por uma pistola 9 mm?

Resposta: $\dpi{100} \inline \mathbf{v_{m}=290\, \, m/s \, \, \, \, \, ou \, \, \, \, \, 1.044\, \, km/h}$

E a velocidade média de um avião de passageiros para voos internacionais?

Resposta: $\dpi{100} \inline\mathbf{v_{m}=250\, \, m/s \, \, \, \, \, ou \, \, \, \, \, 900\, \, km/h}$

Imagine que você seja um piloto desses aviões e durante um determinado voo se depara com outro avião de mesmo porte vindo em sua direção, na mesma trajetória e com sentido de movimento oposto ao seu.

Desconsiderando o uso de instrumentos de voo, ou seja, simplesmente no visual, será que é fácil desviar do outro avião?

Fisicamente, como os dois aviões estão se deslocando sob uma mesma trajetória e com sentidos opostos, como estudamos acima, a velocidade relativa entre os dois aviões será a soma entre suas velocidades, ou seja: v_r = 900 + 900 = 1800 km/h?!?!?!?!

Pois é, comparando as velocidades dos aviões com a da pistola 9 mm, observamos que será mais fácil desviar do “tiro” da pistola do que desviar do outro avião!!!!!

Vamos ver o outro extremo em termos de velocidade relativa.

Imagine agora que os dois aviões acima referidos estejam lado a lado com trajetórias paralelas e voando no mesmo sentido. O que aconteceria com a velocidade relativa?

Fisicamente, como estudamos acima, subtraímos as velocidades, ou seja: v_r = 900 – 900 = 0 km/h?!?!?!?!

Sim, um avião, em relação ao outro, está em repouso.

Um exemplo disso é a foto que está postada no topo desta página, onde um avião carregado de combustível abastece um caça em pleno voo.

Isso é possível exatamente pelo motivo que, independentemente da velocidade dos aviões, a velocidade relativa entre os mesmos é nula.

Para reforçar:

É importantíssimo definir em qual referencial vamos trabalhar antes de começar resolver qualquer problema de Física.

Exercícios Resolvidos

01 – (FisMática) Um trem de cargas com 80 m de comprimento, está viajando a 72 km/h e em determinado instante, terá que passar por uma ponte com 300 m de comprimento. Determine o tempo que o trem gasta para atravessar totalmente a ponte.

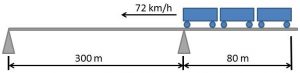
Resolução:

A primeira coisa a se fazer é acertar as unidades. Vamos transformar a velocidade em m/s.

$\dpi{100} \inline \mathbf{v=72\, \, km/h=72\div 3,6=20\, \, m/s}$ (o fator 3,6 foi visto em Aula 02)

Para atravessar totalmente a ponte, a traseira do trem deve atingir o outro lado da mesma. Portando o deslocamento deve ser igual ao comprimento do trem mais o comprimento da ponte:

$\dpi{100} \mathbf{v=\frac{\Delta s}{\Delta t}\rightarrow \Delta t=\frac{\Delta s}{v}=\frac{(200+50)}{10}=\frac{250}{10}=25\ s}$

02 – (FisMática) Dois trens de comprimentos 80 e 70 m, se deslocam a uma velocidade de 54 km/h em sentidos opostos e trilhos distintos.

Determine o tempo de passagem total entre eles.

Resolução:

Vamos inicialmente acertar as unidades transformando a velocidade em m/s:

$\dpi{100} \mathbf{v=54\, km/h=54/3,6=15\, m/s}$

A velocidade relativa é a soma das duas velocidades, pois os trens se deslocam em sentidos opostos:

$\dpi{100} \mathbf{v_{rel}=v_{1}+v_{2}=15+15=30\, m/s}$

Para se obter a passagem total de um trem pelo outro, o deslocamento relativo deve ser igual a soma de seus comprimentos:

$\dpi{100} \mathbf{\Delta s_{rel}=80+70=150\, \, m}$

Cálculo do tempo relativo:

$\dpi{100} \mathbf{\Delta t_{rel}=\Delta s_{rel}\div \Delta s_{rel}=150\div 30={ 5\, \, s}}$

03 – (FisMática) Dois amigos, Carlos e Paulo, estão viajando por uma rodovia no mesmo sentido em dois carros distintos. As 9 h da manhã, Carlos que é mais tranquilo e viaja a 80 km/h, ao passar pelo km 90, liga para Paulo, que é mais apressadinho e viaja a 110 km/h, no exato momento em que ele se encontra no km 30, combinando para se encontrarem mais a frente. Considerando que os dois permaneçam viajando, cada qual, com a velocidade média igual a do momento da ligação, determine o instante e a posição do encontro.

Resolução:

Para efeito de estudo, vamos resolver o problema de duas formas.

1 – Utilizando o conceito de velocidade relativa.

Distância relativa: $\dpi{100} \inline \mathbf{\Delta s_{rel}=km\,90-km\,30=km\,60}$

Velocidade relativa: $\dpi{100} \inline \mathbf{v_{rel}=110-80=30\, \, km/h}$

Tempo relativo: $\dpi{100} \inline \mathbf{\Delta t_{rel}=\Delta s_{rel}\div\Delta s_{rel}=60\div30=2\, \, h}$

Instante em que acontece o encontro: t_e = t₀ + t_rel = 9 + 2 = 11 h, ou seja, eles vão se encontra as 11 h da manhã.

Posição do encontro:

(Carlos) s_e = 90 + 80×2 = 90 + 160 = 250 km
(Paulo) s_e = 30 + 110×2 = 30 + 220 = 250 km

Ou seja, o encontro se dará as 11 h da manhã no km 250 da rodovia.

2 – Utilizando as equações horárias dos movimentos

Vamos considerar o marco zero como origem do sistema de referência.

Equações horárias: ( $\dpi{100} \mathbf{s = s_{0} + v.t}$ )

Carlos: s_C = 90 + 80.t
Paulo: s_P = 30 + 110.t

Encontro:

s_C = s_P => 90 + 80.t = 30 + 110.t => 80.t – 110.t = 30 – 90 => – 30.t = – 60 => t = 2 h

Instante em que acontece o encontro: te = 9 + 2 = 11 h, ou seja, eles vão se encontra as 11 h da manhã.

Substituindo em qualquer uma das equações:

s_C = 90 + 80×2 = 90 + 160 = 250 km ou

s_P = 30 + 110×2 = 30 + 220 = 250 km

Ou seja, o encontro se dará as 11 h da manhã no km 250 da rodovia.

04 – (UFRJ-RJ) Dois trens, um de carga e outro de passageiros, movem-se nos mesmos trilhos retilíneos, em sentidos opostos, um aproximando-se do outro, ambos com movimentos uniformes. O trem de carga, de 50 m de comprimento, tem uma velocidade de módulo igual a 10 m/s e o de passageiros, uma velocidade de módulo igual a v. O trem de carga deve entrar num desvio para que o de passageiros possa prosseguir viagem nos mesmos trilhos, como ilustra a figura. No instante focalizado, as distâncias das dianteiras dos trens ao desvio valem 200 m e 400 m, respectivamente.

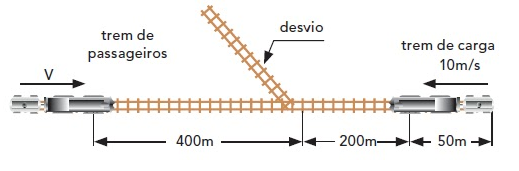
Calcule o valor máximo de v para que não haja colisão.

Resolução:

É lógico que para não haver colisão, quando o trem de passageiros chegar ao desvio, o trem de carga deve estar totalmente dentro do mesmo (desvio).

Vamos resolver como que fossem dois problemas distintos.

Primeiro vamos calcular o tempo para que o trem de carga entre totalmente no desvio.

$\dpi{100} \mathbf{v=\frac{\Delta s}{\Delta t}\rightarrow \Delta t=\frac{\Delta s}{v}=\frac{(200+50)}{10}=\frac{250}{10}=25\ s}$

Segundo, vamos utilizar o tempo calculado acima para sincronizarmos o trem de passageiros.

$\dpi{100} \mathbf{v=\frac{\Delta s}{\Delta t}=\frac{400}{25}=16\; m/s}$

Portanto, o valor máximo de v para que não haja colisão é de 16 m/s.

05 – (FUVEST-SP) João está parado em um posto de gasolina quando vê o carro de seu amigo, passando por um ponto P, na estrada, a 60 km/h. Pretendendo alcançá-lo, João parte com seu carro e passa pelo mesmo ponto P, depois de 4 minutos, já a 80 km/h. Considere que ambos dirigem com velocidades constantes. Medindo o tempo, a partir de sua passagem pelo ponto P, João deverá alcançar seu amigo, aproximadamente, em

a) 4 min b) 10 min c) 12 min d) 15 min e) 20 min

Resolução:

Obs.: inicialmente vamos transformar o tempo em horas: 4 min = (4/60) h.

Vamos considerar o ponto P como origem do sistema. Assim sendo, as equações horárias são:

Amigo: s_A = 60.t_A
João: s_J = 80.t_J

Devemos levar em consideração que há uma diferença nos tempos:

t_A = t_J + 4 min => t_A = t_J + (4/60)

No encontro:

s_J = s_A => 80.t_J = 60.t_A

Passando tudo para t_J:

80.t_J = 60.[t_J + (4/60)] => 80.t_J= 60.t_J + 60.(4/60) => 80.t_J = 60.t_J + 4

Isolando t_J:

80.t_J – 60.t_J = 4 => 20. t_J = 4 => t_J = (4/20) h

Transformando em minutos:

t_J = (4/20)x60 min = 12 min (alternativa c)

06 – (FisMática) Uma partícula se move com velocidade constante de 48 m/s no sentido contrário a orientação do sistema de referencia. Considerando que a mesma parte da posição 25 m, podemos afirmar quanto a sua equação horária e tipo de movimento

a) s = 25 + 48.t e movimento retrógrado

b) s = 25 + 48.t e movimento progressivo

c) s = 25 – 48.t e movimento retardado

d) s = 25 – 48.t e movimento retrógrado

e) s = 25 – 48.t e movimento progressivo

Resolução:

A partícula se movimenta no sentido contrário a orientação do sistema de referência sendo considerada negativa, caracterizando um movimento retrógrado. (alternativa d)

Exercícios Propostos

01 – (PUC-SP) Alberto saiu de casa para o trabalho exatamente às 7 h, desenvolvendo, com seu carro, uma velocidade constante de 54 km/h. Pedro, seu filho, percebe imediatamente que o pai esqueceu sua pasta com documentos e, após 1min de hesitação, sai para encontrá-lo, movendo-se também com velocidade constante. Excelente aluno em Física, calcula que como saiu 1 min após o pai, demorará exatamente 3 min para alcançá-lo. Para que isso seja possível, qual a velocidade escalar do carro de Pedro?

a) 60 km/h

b) 66 km/h

c) 72 km/h

d) 80 km/h

e) 90 km/h

02 – (PUC-RS) Dois móveis, A e B, percorreram uma trajetória retilínea conforme as equações horárias S_A = 30 + 20t e S_B = 90 – 10t, sendo a posição S em metros e o tempo t em segundos. No instante t = 0 s, a distância, em metros, entre os móveis era de:

a) 30 b) 50 c) 60 d) 80 e) 120

03 – (PUC-RS) O instante de encontro, em segundos, entre os dois móveis do exercício anterior foi:

a) 1 b) 2 c) 3 d) 4 e) 5

04 – (FUVEST-SP) Marta e Pedro combinaram encontrar-se em um certo ponto de uma autoestrada plana, para seguirem viagem juntos. Marta, ao passar pelo marco zero da estrada, constatou que, mantendo uma velocidade média de 80 km/h, chegaria na hora certa ao ponto de encontro combinado. No entanto, quando ela já estava no marco do quilômetro 10, ficou sabendo que Pedro tinha se atrasado e, só então, estava passando pelo marco zero, pretendendo continuar sua viagem a uma velocidade média de 100 km/h. Mantendo essas velocidades, seria previsível que os dois amigos se encontrassem próximos a um marco da estrada com indicação de

a) km 20

b) km 30

c) km 40

d) km 50

e) km 60

05 – (MACK-SP) Uma partícula descreve um movimento uniforme cuja função horaria é s = –2 + 5.t, para s em metros e t em segundos. Nesse caso podemos afirmar que a velocidade escalar da partícula é

a) -2 m/s e o movimento é retrógrado

b) -2 m/s e o movimento é progressivo

c) 5 m/s e o movimento é progressivo

d) 5 m/s e o movimento é retrógrado

e) -2,5 m/s e o movimento é retrógrado

06 – (UFSE) No movimento retilíneo uniforme, a distância percorrida é:

a) proporcional ao tempo de percurso

b) proporcional ao quadrado do tempo de percurso

c) inversamente proporcional ao tempo de percurso

d) inversamente proporcional ao quadrado do tempo de percurso

e) proporcional à massa do corpo

07 – (UEPI) Um passageiro perdeu um ônibus que saiu da rodoviária há 5 minutos e pega um táxi para alcançá-lo. O ônibus desenvolve uma velocidade de 60 km/h e o táxi, de 90 km/h. O intervalo de tempo necessário ao táxi para alcançar o ônibus é, em minutos:

a) 10 b) 20 c) 30 d) 32 e) 35

08 – (UFES) Um atirador ouve o ruído da bala atingindo um alvo 3 s após dispará-la com velocidade de 680 m/s. Sabendo que a velocidade do som é de 340 m/s, a distância, em metros, entre o atirador e o alvo é de:

a) 340 b) 680 c) 1.020 d) 1.530 e) 2.040

09 – (FisMática) Dois móveis, A e B, percorreram uma trajetória retilínea conforme as equações horárias S_A = 60 – 20.t e S_B = – 190 + 30.t, sendo a posição S em metros e o tempo t em segundos. O instante e a posição do encontro entre os móveis é

a) t = 5 s e s = 40 m

b) t = 4 s e s = – 40 m

c) t = 4 s e s = 40 m

d) t = 5 s e s = – 40 m

e) t = 5 s e s = – 60 m

10 – (UEL-PR) Duas cidades, A e B, distam entre si 400 km. Da cidade A parte um móvel P dirigindo-se à cidade B e, no mesmo instante, parte de B outro móvel Q, dirigindo-se a A. Os móveis P e Q executam movimentos uniformes e suas velocidades escalares são de 30 km/h e 50 km/h, respectivamente. A distância da cidade A ao ponto de encontro dos móveis P e Q, em quilômetros, vale:

a) 120 b) 150 c) 200 d) 240 e) 250

11 – (FGV-SP) De duas cidadezinhas ligadas por uma estrada reta de 10 km de comprimento, partem simultaneamente, uma em direção a outra, duas carroças, puxadas cada uma por um cavalo e andando a velocidade de 5 km/h. No instante de partida, uma mosca, que estava pousada na testa do primeiro cavalo, parte voando em linha reta, com a velocidade de 15 km/h e vai pousar na testa do segundo cavalo. Após um intervalo de tempo desprezível, ela parte novamente e volta, com a mesma velocidade de antes, em direção ao primeiro cavalo, até pousar em sua testa. E assim prossegue nesse vaivém até que os dois cavalos se encontram e a mosca morre esmagada entre as duas testas. Quantos quilômetros percorreu a mosca?

Gabarito

Ex. 01 – alternativa c.

Ex. 02 – alternativa c.

Ex. 03 – alternativa b.

Ex. 04 – alternativa d.

Ex. 05 – alternativa c.

Ex. 06 – alternativa a.

Ex. 07 – alternativa a.

Ex. 08 – alternativa b.

Ex. 09 – alternativa d.

Ex. 10 – alternativa b.

Ex. 11 – A distância percorrida é de 15 km.

Deixe uma resposta Cancelar resposta

Você precisa fazer o login para publicar um comentário.

F1_DG_Aula 05 – MRU: Velocidade Relativa

1 – Dois corpos se movimentando no mesmo sentido

2 – Dois corpos se movimentando em sentidos opostos

3 – Um corpo em movimento e outro em repouso

Curiosidades

Exercícios Resolvidos

Exercícios Propostos

Gabarito

Deixe uma resposta Cancelar resposta

Faça login com sua conta de site

Registre uma nova conta

Modal title