F2_DG_Aula 04 – Função Termométrica

Existem vários tipos de termômetros com precisões e aplicações diversas.

Os mais conhecidos são os que utilizam a expansão do volume de um líquido, como o álcool ou mercúrio, que através de uma escala apropriada e feita a calibração, nos indica a temperatura de um corpo ou ambiente que desejamos medir.

Em laboratórios são utilizados termômetros a gás que são divididos em dois tipos de acordo com o princípio de funcionamento:

Mantendo o volume constante e calibrando a escala de temperatura em função da pressão exercida pelo gás devido as variações de temperaturas;
Mantendo a pressão constante e calibrando a escala de temperatura em função do volume assumido pelo gás devido as variações de temperaturas;

Existem ainda termômetros que utilizam resistência elétrica, barras metálicas, etc.

Seja qual for o tipo de termômetro utilizado, há a necessidade de se correlacionar a temperatura e o tipo de grandeza que está sendo utilizada, a qual denominamos de Função Termométrica.

Normalmente função termométrica é do 1º grau tendo como gráfico uma reta (para saber mais, veja a Aula 06 da Cinemática Escalar).

Para exemplificar vamos utilizar a relação entre as escalas Celsius e Kelvin, que já foi vista anteriormente.

Função do 1º grau: y = a.x + b

Relação das escalas: t_K = t_C + 273 (t_K > 0)

Por comparação:

Parâmetros a e b: a = 1 e b = 273

Variáveis y e x: y = t_K e x = t_C

Graficamente temos (sem escala):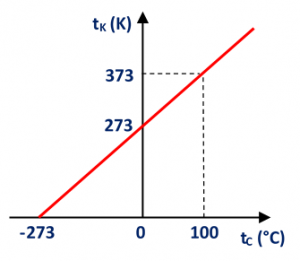

Obs.: nos exercícios resolvidos será montada uma equação entre escalas a partir do gráfico que as relacionam.

Uma Escala Qualquer

A princípio, com base em uma escala conhecida, podemos montar uma escala qualquer, de acordo com aplicações ou mesmo por gosto.

Para exemplificar, será montada uma escala FisMática (°M, para diferenciar da Fahrenheit), em relação à escala Celsius.

Vamos considerar as temperaturas de 20 °M para o ponto de gelo, 80 °M para o ponto de vapor e dividir a escala em 60 partes iguais.

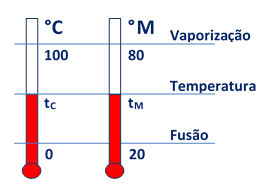
Utilizando as regras de proporção, matematicamente obtemos as seguintes relações:

$\dpi{100} \small {{\color{Emerald} } \mathbf{\frac{t_{C}-0}{100-0}=\frac{t_{M}-20}{80-20}}}$

Com um pouco de álgebra se chega a relação final entre as duas escalas:

$\dpi{100} \small {{\color{Emerald} } \mathbf{\frac{t_{C}}{5}=\frac{t_{M}-20}{3}}}$

Exemplo: determine a temperatura na escala FisMática equivalente a 30 °C.

Multiplicando a última relação em cruz, temos:

5.(t_M – 20) = 3.t_C

Substituindo o valor de 30 °C na variável t_C temos:

5.(t_M – 20) = 3×30 => t_M – 20 = 90/5

t_M = 18 + 20 => t_M = 38 °M

Exercícios Resolvidos

01 – (FisMática) Um aluno chamado Renan resolveu criar uma escala termométrica e batizá-la com seu nome, denominando a graduação da mesma de °R. Para compor a escala de sua escala, ele comparou com a escala Celsius apresentando os resultados na forma de um gráfico como mostra a figura abaixo.

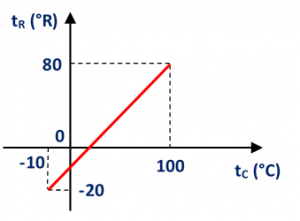
Com base no gráfico, determine:

a relação entre as duas escalas;
o valor da temperatura em °R equivalente a 30 °C.

Resolução:

a) Como a relação entre as duas escalas é representada por uma reta, as razões entre dois intervalos relativos são iguais. Utilizando este fato, temos:

$\dpi{100} \small {{\color{Emerald} } \mathbf{\frac{t_{R}-(-20)}{80-(-20)}=\frac{t_{C}-(-10)}{100-(-10)}\rightarrow \frac{t_{R}+20}{80+20}=\frac{t_{C}+10}{100+10}}}$

$\dpi{100} \small {{\color{Emerald} } \mathbf{\frac{t_{R}+20}{100}=\frac{t_{C}+10}{110}\rightarrow {\color{Red} \frac{t_{R}+20}{10}=\frac{t_{C}+10}{11}}}}$

b) Fazendo t_C = 30 °C na relação obtida no item a, temos:

$\dpi{100} \small {{\color{Emerald} } \mathbf{\frac{t_{R}+20}{10}=\frac{30+10}{11}\rightarrow \frac{t_{R}+20}{10}=\frac{40}{11}}}$

Multiplicando em “cruz” e com um pouco de álgebra, temos:

11.(t_R + 20) = 10×40 => 11.t_R + 220 = 400 => 11.t_R = 180

Isolando t_R:

t_R = 180:11 => t_R = 16,4 °R

02 – (MACK – SP) Na escala termométrica X, ao nível do mar, a temperatura do gelo fundente é -30 °X e a temperatura de ebulição da água é 120 °X. A temperatura na escala Celsius que corresponde a 0 °X é:

a) 15 °C b) 20 °C c) 25 °C d) 28 °C e) 30 °C

Resolução:

A base da solução do problema é a mesma utilizada no problema anterior. Vamos utilizar a proporção entre as escalas e já substituir os valores do enunciado, lembrando que na escala Celsius a água se funde a 0 °C e se evapora a 100 °C.

$\dpi{100} \small {{ \color{Emerald} } \mathbf{ \frac{0-(-30)}{120-(-30)}= \frac{t_{C}-0}{100-0} \rightarrow \frac{30}{150}= \frac{t_{C}}{100}}}$

Multiplicando em “cruz” e com um pouco de álgebra, temos:

150.t_C = 30×100 => t_C = 3000:150 => t_C = 20 °C (alternativa b)

Exercícios Propostos

01 – (UNIBAN-SP) Ao utilizar um termômetro de mercúrio para medir a temperatura de uma pessoa, um médico percebeu que a escala do instrumento estava apagada entre os valores 36,5 °C e 40 °C. Para saber a temperatura do paciente, o médico mediu o comprimento da escala do instrumento (de 35 °C a 45 °C), encontrando 5,0 cm. Em seguida mediu a altura da coluna de mercúrio correspondente à temperatura da pessoa, encontrando 1,5 cm. Qual a temperatura determinada pelo médico?

a) 18 °C

b) 26 °C

c) 24 °C

d) 30 °C

e) 38 °C

02 – (UNIFOR-CE) Um estudante resolveu criar uma escala E de temperaturas e, comparando-a com a escala Celsius, obteve o gráfico abaixo.

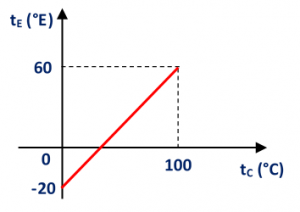
Na escala E do estudante, a temperatura do corpo humano é mais próxima de:

a) 25 °E

b) 20 °E

c) 15 °E

d) 10 °E

e) 5 °E

03 – (UFAL) Um termômetro A foi calibrado de modo que o ponto de gelo corresponde a 2 °A e o ponto de ebulição da água corresponde a 22 °A. Esse termômetro de escala A e um termômetro de escala Celsius indicarão o mesmo valor para a temperatura de:

a) 25

b) 13

c) 7,5

d) 5,0

e) 2,5

04 – (ITA) Para medir a febre de pacientes, um estudante de medicina criou sua própria escala linear de temperaturas. Nessa nova escala, os valores de 0 (zero) e 10 (dez) correspondem respectivamente a 37 °C e 40 °C. A temperatura de mesmo valor numérico em ambas escalas é aproximadamente:

a) 52,9 °C

b) 28,5 °C

c) 74,3 °C

d) –8,5 °C

e) –28,5 °C

05 – (UF-Londrina) Uma escala termométrica E adota os valores –10 °E para o ponto de gelo e 240°E para o ponto de vapor. Qual a indicação que na escala E corresponde a 30 °C?

a) 55 °E

b) 65 °E

c) 66 °E

d) 54 °E

e) 38 °E

06 – (MACK-SP) Ao nível do mar, mediante os termômetros, um graduado da escala Celsius e outro na escala Fahrenheit, determinamos a temperatura de certa massa de água líquida. A diferença entre as leituras dos dois termômetros é 100. A temperatura dessa massa de água na escala Kelvin é:

a) 85 K

b) 108 K

c) 273 K

d) 358 K

e) 438 K

07 – (MACK-SP) O quíntuplo de uma certa indicação de temperatura registrada num termômetro graduado na escala Celsius excede em 6 unidades o dobro da correspondente indicação na escala Fahrenheit. Esta temperatura, medida na escala Kelvin, é de:

a) 50 K

b) 223 K

c) 273 K

d) 300 K

e) 323 K

08 – (MACK-SP) Um termômetro mal graduado na escala Celsius, assinala 2 °C para a fusão da água e 107 °C para sua ebulição, sob pressão normal. Sendo θ_E o valor lido no termômetro mal graduado e θ_C o valor correto da temperatura, a função de correção do valor lido é:

a) θ_C= (50/51) (θ_E-2)

b) θ_C= (20/22) (2.θ_E -1)

c) θ_C= (30/25) (θ_E-2)

d) θ_C= (20/21) (θ_E -2)

e) θ_C= (21/20) (θ_E-4)

09 – (FATEC-SP) Uma escala termométrica arbitrária X atribui o valor -20 °X para a temperatura de fusão do gelo e 120 °X para a temperatura de ebulição da água, sob pressão normal. A temperatura em que a escala X dá a mesma indicação que a Celsius é:

a) 80

b) 70

c) 50

d) 30

e) 10

10 – (UFBA) As indicações para o ponto de fusão do gelo e de ebulição da água sob pressão normal de dois termômetros, um na escala Celsius e outro na escala Fahrenheit, distam 20 cm, conforme a figura.

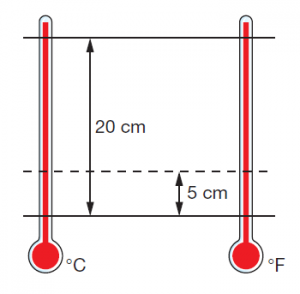
A 5 cm do ponto de fusão do gelo, os termômetros registram temperaturas iguais a:

a) 25 °C e 77 °F

b) 20 °C e 40 °F

c) 20 °C e 45 °F

d) 25 °C e 45 °F

e) 25 °C e 53 °F

11 – (UNIFOR-CE) Uma escala de temperatura arbitrária X está relacionada com a escala Celsius de acordo com o gráfico abaixo.

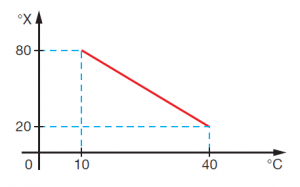
As temperaturas de fusão do gelo e de ebulição da água, sob pressão normal, na escala X valem, respectivamente:

a) – 100 e 50

b) – 100 e 0

c) – 50 e 50

d) 100 e – 100

e) 100 e 50

Gabarito

Ex. 01 – alternativa e.

Ex. 02 – alternativa d.

Ex. 03 – alternativa e.

Ex. 04 – alternativa a.

Ex. 05 – alternativa b.

Ex. 06 – alternativa d.

Ex. 07 – alternativa e.

Ex. 08 – alternativa d.

Ex. 09 – alternativa c.

Ex. 10 – alternativa d.

Ex. 11 – alternativa d.

Deixe uma resposta Cancelar resposta

Você precisa fazer o login para publicar um comentário.

F2_DG_Aula 04 – Função Termométrica

Uma Escala Qualquer

Exercícios Resolvidos

Exercícios Propostos

Gabarito

Deixe uma resposta Cancelar resposta

Faça login com sua conta de site

Registre uma nova conta

Modal title