M3_DG_Aula 01 – Noções e Proposições Primitivas
Noções Primitivas
Os conceitos, entes ou termos, podem ser simplesmente denominados de Noções Geométricas, as quais são estabelecidas por meio de Definição.
Em matemática existem as Noções Primitivas, que não são definidas e, sim, simplesmente adotadas como verdadeiras.
Como base da Geometria Plana, serão adotadas sem definição as noções de: Ponto, Reta e Plano
Apesar de não serem definidos, todo estudante tem a exata noção do que representam os três entes acima citados.
Uma vez apresentados, podemos começar construir a nossa geometria.
Podemos dar nome aos entes utilizando letras ou representar os mesmos na forma gráfica.
1 – Utilizando letras:
- Pontos: são representados por letras latinas maiúsculas: A, B, C, …
- Retas: são representadas por letras latinas minúsculas: a, b, c, …
- Planos: são representados por letras gregas minúsculas: α, β, ϒ, …
2 – Utilizando notações gráficas:
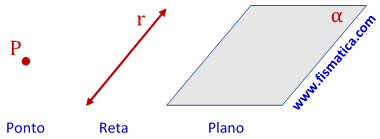
Proposições Primitivas
As propriedades e afirmações, são denominadas Proposições Geométricas e são aceitas mediante demonstrações.
As Proposições Primitivas ou Axiomas ou Postulados, são simplesmente aceitas, ou seja, não necessitam de demonstração.
Vamos dar início aos estudos da Geometria Plana com alguns postulados envolvendo ponto, reta e plano.
Postulado de Existência
- Numa reta existem infinitos pontos
- Fora da reta também existem infinitos pontos
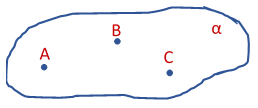
- Num plano existem infinitos pontos
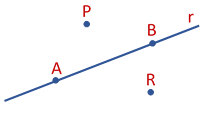Observando a figura acima, verificamos que:
- Os pontos A e B pertencem a reta r (A
r e B
- Os pontos P e R não pertencem a reta r (P
r e R
Posições entre Pontos e Retas
Dados dois pontos A e B, podemos ter duas possibilidades:
- A e B são coincidentes (é um único ponto com dois nomes)
- A e B são distintos
Graficamente, temos que:
Dados um ponto P e uma reta r, podemos ter duas possibilidades:
- P pertence a reta r (P
- P não pertence a reta r (P
Graficamente, temos que:
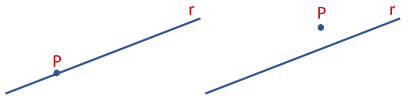
Nota: quando vários pontos pertencem a uma determinada reta, dizemos que os mesmos são Colineares. Podemos dizer que pontos colineares são “pontos alinhados”.
Postulado da Determinação
1 – Para a Reta
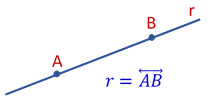
“Dois pontos distintos determinam uma única, e somente uma, reta que passa pelos mesmos.”
Dados dois pontos distintos A e B, eles definem uma única reta que representamos por: .
Ou seja:
Graficamente, temos que:
2 – Para o Plano
“Três pontos distintos e não colineares determinam um único, e somente um, plano que passa pelos mesmos.”
Graficamente, temos que:
Postulado da Inclusão
Para a Reta
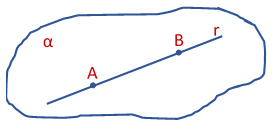
“Se determinada reta tem dois pontos distintos pertencentes a um plano, a própria reta está contida nesse plano.”
Dados dois pontos distintos A e B de um plano α, a reta r = tem todos os seus pontos no plano.
Ou seja:
Graficamente, temos que:
Notas:
- Pontos Coplanares: pertencem a um mesmo plano
- Figura: qualquer conjunto de pontos
- Figura Plana: é toda figura que tem todos os seus pontos num mesmo plano
Obs.: a Geometria Plana estuda as Figuras Planas.
Posições Relativas entre duas Retas
1 – Concorrentes
“Duas retas r e s são ditas concorrentes, se e somente se, elas têm um único ponto em comum.”
Graficamente, temos que:
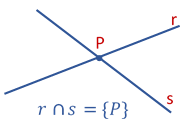
Nota: no caso particular em que os ângulos entre as duas retas formam 90°, elas são ditas perpendiculares entre si .
2 – Paralelas
“Duas retas r e s são ditas paralelas, se e somente se, elas não têm nenhum ponto em comum.”
Graficamente, temos que:
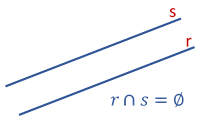
3 – Coincidentes
“Duas retas r e s são ditas coincidentes, se e somente se, elas têm todos os pontos em comum.”
Graficamente, temos que:
Exercícios Resolvidos
01 – (FisMática) Quantos pontos em comum tem duas retas reversas coplanares?
a) 2 b) 0 c) 3 d) 1 e) 4
Resolução:
Por definição, duas retas reversas têm apenas um ponto em comum (alternativa d)
02 – (FisMática) Por definição, toda reta é composta por … pontos?
a) 2 b) 0 c) ∞ d) 1 e) nda
Resolução:
Por definição, toda reta é composta por infinitos pontos (alternativa c)
Exercícios Propostos
01 – (FisMática) Considere as afirmações a seguir:
I – As Retas são representadas por letras latinas maiúsculas: A, B, C, …
II – Os pontos são representados por letras latinas minúsculas: a, b, c, …
III – Os Planos são representados por letras gregas minúsculas: α, β, ϒ, …
Podemos afirmar que:
a) Apenas I e II são verdadeiras
b) Apenas II e III são verdadeiras
c) Todas são falsas
d) Apenas a III é verdadeira
e) Todas são verdadeiras
02 – (FisMática) Quantos pontos, no mínimo, são necessários para definir um plano?
a) 3 b) 1 c) ∞ d) 2 e) nda
03 – (FisMática) Assinale a alternativa correta:
a) Duas retas paralelas se encontram no infinito.
b) Duas retas paralelas se encontram em um único ponto.
c) Duas retas reversas não têm nenhum ponto em comum.
d) Duas retas congruentes têm apenas dois pontos em comum.
e) Duas retas perpendiculares entre si também são reversas.
04 – (FisMática) Quais das definições a seguir são aceitas sem demonstração:
I – Proposições
II – Axiomas
III – Postulados
a) Apenas a I b) Apenas a II e a III c) Nenhuma d) Apenas a III e) Todas
05 – (FisMática) Quando vários pontos pertencem a uma determinada reta, dizemos que eles são:
a) Coplanares b) Colineares c) Postulados d) Congruentes e) Divergentes
Gabarito
Ex. 01 – alternativa d.
Ex. 02 – alternativa a.
Ex. 03 – alternativa e.
Ex. 04 – alternativa b.
Ex. 05 – alternativa b.