M3_Aula 02 – Retas
Na aula anterior, foi dito que em matemática existem as “Noções Primitivas, que não são definidas e, sim, simplesmente adotadas como verdadeiras”.
Portanto, não vamos definir o que é uma Reta e, sim, aceitar como sendo um conceito primitivo.
Vamos elencar a seguir algumas características das retas:
- São figuras geométricas compostas por infinitos pontos
- São infinitas
- Podem ser traçadas a partir de dois pontos distintos
- Entre dois de seus pontos, sempre existe um terceiro ponto pertencente a ela
- Três pontos colineares sempre pertencem a uma mesma reta
- Definem uma direção
Segmento de Reta
Quando tomamos dois pontos quaisquer pertencentes a uma determinada reta, podemos imaginar que estamos “cortando um pedaço” dessa reta, ou seja, estamos definindo um Segmento de Reta.
A figura a seguir exibe uma reta r e dois pontos A e B, pertencentes a ela, definindo sobre a mesma o Segmento de Reta AB, que simbolicamente é representado pelas duas letras que definem os dois pontos com um traço sobre elas.
![]()
“Dados dois pontos distintos pertencentes a uma reta, a união do conjunto desses dois pontos com o conjunto de todos os pontos que estão entre eles define um segmento de reta.”
Numa representação matemática, temos que:
Como observamos, os pontos A e B são as extremidades do segmento e X representa um ponto interno essas extremidades.
Nota: se os pontos A e B forem coincidentes (não distintos), dizemos que o segmento é um Segmento Nulo.
Semirreta
Se tomarmos uma reta r e marcarmos um ponto sobre ela, na prática, podemos dizer que esse ponto “divide a reta r em duas partes”.
Sem utilizar ainda, uma formalidade matemática, dizemos que “a reta r foi dividida em duas semirretas”.
![]()
Agora que entendemos a ideia de semirreta, vamos formalizar seu conceito.
“Dados dois pontos distintos, A e B, pertencentes a uma reta r, a união do segmento de reta
, com o conjunto dos pontos X, tais que, B está entre A e X, define a semirreta
.”
Numa representação matemática, temos que:
A figura a seguir exibe uma reta r, o segmento de reta e os pontos X e Y, não pertencentes ao segmento
, definindo as Semirretas
, que simbolicamente são representadas pelas duas letras que a definem com uma seta sobre elas.

Notem que, diferentemente dos segmentos de reta, as semirretas têm sentido, porém, a seta sobre as letras que as representam, é apenas um símbolo e não acompanha os sentidos delas.
No exemplo dado, as semirretas tem sentidos opostos e, portanto, são denominadas de Semirretas Opostas.
Dando sequência ao nosso estudo dos segmentos, preparando a base para estudar as figuras geométricas planas, vamos classificar os segmentos em três categorias: Colineares, Consecutivos e Adjacentes.
Segmentos Consecutivos
“Dois segmentos de reta são ditos Consecutivos, se e somente se, tiverem uma das extremidades em comum.”
Exemplos:
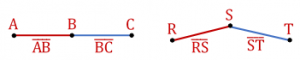
Nota: não obrigatoriamente dois segmentos consecutivos têm que estar sobre uma mesma reta.
Segmentos Colineares
Já vimos que pontos colineares, por definição, pertencem a uma mesma reta.
Seguindo o mesmo raciocínio, temos que:
“Dois segmentos são ditos colineares, se e somente se, pertencem a uma mesma reta.”
Exemplos:
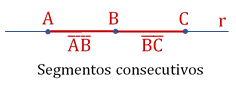
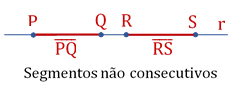
Como podemos observar das figuras, os seguimentos colineares podem ou não serem consecutivos.
Segmentos Adjacentes
Observem as figuras a seguir:
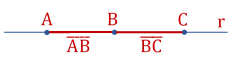
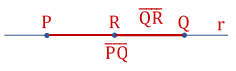
Notem que em cada uma das figuras, existem dois segmentos consecutivos, com a diferença de que, na primeira, segmentos , só têm um ponto em comum ( B ), enquanto que, na segunda, segmentos
, todos os pontos do segmento
, são comuns ao segmento
.
Por definição:
“Dois segmentos de reta são ditos Adjacentes, se e somente se, forem consecutivos, colineares e tiverem apenas uma das extremidades em comum.”
Portanto:
- Os segmentos
são adjacentes
- Os segmentos
não são adjacentes
Segmentos Congruentes
Em geometria, quando temos “segmentos iguais”, denominamos de Segmentos Congruentes, sendo utilizado o símbolo .
Quando dois segmentos são ditos congruentes, eles obedecem a três postulados:
- Simetria: se
, então
- Reflexiva: qualquer segmento é congruente a si mesmo
- Transitiva: se
, então
Graficamente, para dizer que dois, ou mais, segmentos são congruentes, utilizamos um “risquinho” nos segmentos, como mostra a figura a seguir:
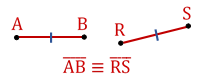
Ponto Médio e Comprimento de um Segmento
Ponto Médio
Dado um segmento , o ponto médio (M), estará entre os pontos Q e será equidistante dos mesmos.
Na forma matemática, temos que:
Se M é o ponto médio do segmento , então: .
![]()
Comprimento ou Medida de um Segmento
O Comprimento ou Medida de um Segmento é representado por
ou simplesmente AB.
A medida de um segmento não nulo, está associado a um número real, cuja unidade pode ser: m, cm, mm, km, etc.
Para encerrar essa aula, vamos definir a distância entre dois pontos (dAB).
Dado um Segmento , podemos ter duas definições de distância:
1 – Distância Geométrica: é o comprimento do segmento .
2 – Distância Métrica: é o número associado ao comprimento do segmento .
Exercícios Resolvidos
01 – (FisMática) Justifique cada uma das afirmativas a seguir:
a) Dois pontos distintos determinam uma única reta.
Para se definir uma reta, é preciso de pelo menos dois pontos e uma vez definida, ela é única. Portanto, podemos dizer que a afirmativa é verdadeira.
b) Por três pontos dados passa uma só reta.
Por três pontos colineares passa uma única reta. No enunciado não é dito que os três pontos dados são colineares. Portanto, podemos dizer que a afirmativa é falsa.
c) Quatro pontos distintos determinam duas retas.
Se os quatro pontos forem colineares, teremos uma única reta.
Se os quatro pontos não forem colineares, teremos mais do que duas retas.
Por exemplo, na disposição dos pontos conforme figura a seguir, passam 6 retas.
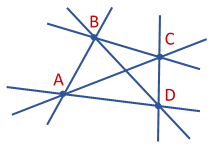
Portanto, podemos dizer que a afirmativa é falsa.
d) Por um ponto passam infinitas retas.
Para se definir uma reta, é preciso de pelo menos dois pontos. Portanto, podemos dizer que a afirmativa é verdadeira.
02 – (FisMática) Sejam A, B e C três pontos distintos pertencentes a uma reta r. Se AB é igual ao dobro de BC e AC = 36 cm, determine as medidas dos segmentos AB e BC.
Resolução:
Podemos ter três posicionamentos dos pontos ABC.
Obs.: as figuras estão sem escala.
1 – O ponto B pode estar antes de A:

Resposta: o enunciado diz que AB é igual ao dobro de BC e observando a figura, vemos que isso não acontece. Portanto, para atender o que é pedido, essa configuração está descartada.
2 – O ponto B pode estar entre A e C:
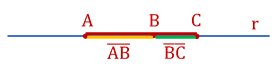
Observando a figura, vemos que: AB + BC = AC
Como, pelo enunciado, AB = 2.BC, substituindo na expressão acima, temos que:
AB + BC = AC => 2.BC + BC = AC => 3.BC = 36 => BC = 12
Resposta: BC = 12 cm e AC = 24 cm
3 – O ponto B pode estar depois de C:

Observando a figura, vemos que: AB = AC + BC
Como, pelo enunciado, AB = 2.BC, substituindo na expressão acima, temos que:
AB = AC + BC => 2.BC = AC + BC => BC = AC => BC = 36
Resposta: BC = 36 cm e AC = 72 cm
Exercícios Propostos
01 – (Dolce/Pompeo-UNICAMP) Indicando se cada afirmação abaixo é verdadeira ou falsa:
( ) Por um ponto passam infinitas retas.
( ) Dois pontos distintos determinam uma única reta.
( ) Por três pontos dados passa uma só reta.
( ) Quatro pontos distintos determinam duas retas.
Assinale a resposta correta.
a) V – V – V – F b) F – V – F – F c) V – V – V – V d) V – V – F – F e) V – F – V – F
02 – (Dolce/Pompeo-UNICAMP) Indicando se cada afirmação abaixo é verdadeira ou falsa:
( ) Uma reta contém dois pontos distintos.
( ) Por três pontos dados passa uma só reta.
( ) Três pontos distintos são sempre coplanares.
( ) Três pontos pertencentes a um plano são sempre colineares.
Assinale a resposta correta.
a) V – V – V – F b) V – F – V – F c) V – V – V – V d) V – V – F – F e) V – F – V – V
03 – (Dolce/Pompeo-UNICAMP) Quantas retas distintas podemos passar por quatro pontos todos distintos, sendo três deles colineares?
a) 1 b) 2 c) 3 d) 4 e) 5
04 – (Dolce/Pompeo-UNICAMP) Dados três pontos A, B e C pertencentes a uma reta r, quantos segmentos distintos têm dois desses pontos como extremos?
a) 1 b) 2 c) 3 d) 4 e) 5
05 – (Dolce/Pompeo-UNICAMP) Indicando se cada afirmação abaixo é verdadeira ou falsa:
( ) Quaisquer que sejam os pontos ? e ?, se ? é distinto de ?, então existe uma reta ?? tal que ? ∈ ? e ? ∈ ?.
( ) Quaisquer que sejam os pontos ? e ?, se ? é distinto de ? , e se ? e ? pertencem tanto à reta ? como à reta ?, então ? = ?.
( ) Qualquer que seja a reta ?, existem dois pontos ? e ? tais que ? é distinto de ?, com ? ∈ ? e ? ∈ ?.
( ) Se ? = ?, existe uma reta ? tal que ? ∈ ? e ? ∈ ?.
Assinale a resposta correta.
a) V – V – V – F b) V – F – V – F c) V – V – V – V d) V – V – F – F e) V – F – V – V
06 – (Dolce/Pompeo-UNICAMP) Dados três pontos A, B e C pertencentes a uma reta r, quantas semirretas há em ? com origem em A, B e C?
a) 4 b) 3 c) 7 d) 5 e) 6
07 – (Dolce/Pompeo-UNICAMP) Indique se cada afirmação abaixo é verdadeira ou falsa:
( ) Se dois segmentos são consecutivos, então eles são colineares.
( ) Se dois segmentos são colineares, então eles são consecutivos.
( ) Se dois segmentos são adjacentes, então eles são colineares.
( ) Se dois segmentos são adjacentes, então eles são consecutivos.
Assinale a resposta correta.
a) F – F – V – V b) V – F – V – F c) V – V – V – V d) V – V – F – F e) V – F – V – V
08 – (Dolce/Pompeo-UNICAMP) Os segmentos AB e BC são adjacentes, o mesmo acontecendo com os segmentos BC e CD. O segmento AB tem o triplo do comprimento de BC, o segmento BC tem o dobro do comprimento de CD, e AD mede 36 cm. As medidas dos segmentos AB, BC e CD, são: AB = 24 cm, BC = 8 cm e CD = 4 cm
a) AB = 21 cm, BC = 10 cm e CD = 5 cm
b) AB = 18 cm, BC = 12 cm e CD = 6 cm
c) AB = 24 cm, BC = 8 cm e CD = 4 cm
d) AB = 24 cm, BC = 8 cm e CD = 4 cm
e) AB = 15 cm, BC = 14 cm e CD = 7 cm
09 – (Dolce/Pompeo-UNICAMP) Indique se cada afirmação abaixo é verdadeira ou falsa:
( ) Se dois segmentos são colineares, então eles são consecutivos.
( ) Se dois segmentos são colineares, então eles são adjacentes.
( ) Se dois segmentos são adjacentes, então eles são consecutivos.
( ) Se dois segmentos são consecutivos, então eles são adjacentes.
Assinale a resposta correta.
a) F – F – V – V b) V – F – V – F c) V – V – V – V d) V – V – F – F e) F – F – V – F
10 – (Dolce/Pompeo-UNICAMP) P, Q e R são três pontos distintos de uma reta. Se PQ é igual ao triplo de QR e PR = 32 cm, as medidas dos segmentos PQ e QR são:
a) PQ = 24 cm e QR = 8 cm, ou PQ = 48 cm e QR = 16 cm
b) PQ = 24 cm e QR = 18 cm, ou PQ = 48 cm e QR = 26 cm
c) PQ = 34 cm e QR = 18 cm, ou PQ = 28 cm e QR = 26 cm
d) PQ = 24 cm e QR = 18 cm, ou PQ = 38 cm e QR = 16 cm
e) PQ = 34 cm e QR = 28 cm, ou PQ = 48 cm e QR = 26 cm
Gabarito
Ex. 01 – alternativa d.
Ex. 02 – alternativa b.
Ex. 03 – alternativa d.
Ex. 04 – alternativa c.
Ex. 05 – alternativa c.
Ex. 06 – alternativa e.
Ex. 07 – alternativa a.
Ex. 08 – alternativa d.
Ex. 09 – alternativa e.
Ex. 10 – alternativa a.
