F1_Aula 01 – CE: Fundamentos
Referencial
Em nosso dia a dia, mesmo sem sabermos, estamos utilizando referenciais quando observamos as coisas que acontecem ao nosso redor.

O referencial em Física é muito mais evidenciado, pois antes de descrevermos um fenômeno físico necessitamos dizer em relação a qual “Referencial” este fenômeno está sendo estudado, o qual pode ser real ou convencional.
Exemplos:
Referencial Real: Para estudar o movimento de um carro que trafega pela Rodovia Anhanguera/SP, será utilizado o Km 20 como referência.

Modelo de Partícula
Obs.: em Física muitas vezes uma Partícula também é denominada Ponto Material.
Quando ouvimos a palavra “Partícula” geralmente pensamos em algo muito pequeno, como por exemplo um elétron, mas, você sabia que a Terra pode ser considerada como uma Partícula? Pois é, vamos ver como isso é possível.
Inicialmente, para entendermos o conceito de Partícula, ou Ponto Material, vamos utilizar como exemplo a própria Terra.
Ao analisarmos o movimento de um avião voando em torno da Terra podemos facilmente verificar que a Terra é “muito grande” comparada com o avião, enquanto que, ao compararmos as dimensões da Terra com as do Sol, verificamos que a Terra é “muito pequena” comparada com o nosso Astro Rei (o Sol é mais de 100 vezes maior do que a Terra).
Quando estudarmos o movimento de translação da Terra em torno do Sol, verificamos que o raio da Terra (6.371 km) é “muito pequeno” comparado com a distância da Terra ao Sol que é em torno de 150 milhões de quilômetros (1 UA – unidade astronômica).
Assim sendo, no primeiro exemplo, as dimensões da Terra devem ser consideradas quando estudamos o movimento de um avião ao seu redor, enquanto que, no segundo exemplo, “as dimensões da Terra são desprezíveis comparadas à distância ao Sol” e, nesse caso, a Terra pode ser considerada como uma Partícula.
Resumindo: quando estudamos o movimento de translação da Terra em torno do Sol, a Terra é considerada como uma Partícula.
Para ilustrar ainda mais o conceito de partícula, vamos ver um outro exemplo bem prático, apresentado na forma de duas situações reais.
Situação 01: suponhamos que você tenha uma garagem “grande” e decida movimentar dentro dela um pequeno caminhão, um carro médio e uma moto, como ilustra a figura a seguir:
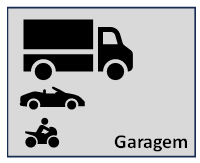
Podemos observar que:
- O caminhão não terá muito espaço para se movimentar;
- O carro já terá algum espaço para se movimentar;
- A moto poderá ser movimentada com certa facilidade.
Portanto, podemos concluir que as dimensões: do caminhão, do carro e da moto, “fazem diferença” na movimentação destes veículos dentro de uma garagem, ou seja, “as dimensões de cada veículo importam perante o problema a ser resolvido”, ou “as dimensões de cada veículo não podem ser desprezadas perante o problema a ser resolvido”.
Situação 02: suponhamos que você e, mais dois amigos, se desloquem entre as cidades de Campinas e São Paulo, no estado de SP, que distam em torno de 100 km uma da outra. Suponhamos ainda que: um vá dirigindo um pequeno caminhão, outro um carro médio e o terceiro pilotando uma moto, como ilustra a figura a seguir:

Podemos observar que, perante os 100 km que serão percorridos, tanto faz ir de caminhão, de carro ou mesmo de moto.
Portanto, podemos concluir que as dimensões: do caminhão, do carro e da moto, “não fazem diferença” na movimentação destes veículos ao serem deslocados por uma distância de 100 km, ou seja, “as dimensões de cada veículo não importam perante o problema a ser resolvido”, ou “as dimensões de cada veículo podem ser desprezadas perante o problema a ser resolvido”.
Finalmente podemos apresentar o conceito de Partícula ou Ponto Material:
Quando as dimensões de um corpo são desprezíveis perante as dimensões do problema em estudo, este corpo pode ser considerado como uma Partícula.
Obs.: no estudo da Cinemática os corpos em movimento são considerados como Partículas.
Movimento e Repouso
Vamos ilustrar os conceitos através de um exemplo:
Consideremos um ônibus que se movimenta em uma rodovia com velocidade constante, digamos a 100 km/h:
Em relação ao ônibus, o motorista está em repouso, enquanto que, em relação a Terra, o mesmo motorista está em movimento.
Completando a informação, se você já viajou de ônibus certamente observou que durante o trajeto por uma rodovia que não tenha muitas curvas acentuadas e que está sendo percorrida com velocidade praticamente constante, as pessoas podem se movimentar dentro do mesmo como se ele estivesse parado.
Conclusão:
Estar em movimento ou repouso depende do referencial adotado.
Obs.: normalmente a nossa noção de movimento e repouso tem como referencial a própria Terra.
Outro exemplo, se uma pessoa estiver dentro de um Transatlântico que está flutuando em mar aberto com águas calmas, caso esta pessoa não consiga olhar para fora e ver o mar, ela não terá condições de saber se o Transatlântico está ancorado (em repouso) ou navegando (em movimento).
Feitas as considerações anteriores, podemos definir o que representa estar em movimento ou repouso em relação a um determinado referencial:
Uma partícula está em movimento, em relação a um determinado referencial, quando sua posição em relação ao mesmo referencial varia com o tempo.
Analogamente:
Uma partícula está em repouso, em relação a um determinado referencial, quando sua posição em relação ao mesmo referencial não varia com o tempo.
Cuidado: note que foi utilizado “posição” e não “distância”, pois, se um corpo gira em torno de um ponto qualquer mantendo o raio constante, ele permanece sempre a mesma distância do ponto, porém, não está em repouso e, sim, em movimento.
Para exemplificar o que foi dito acima, vamos utilizar como exemplo o relógio da figura a seguir:

Podemos observar que há uma marca vermelha na extremidade do ponteiro dos segundos. Se ficarmos vendo o ponteiro dos segundos se movimentar, iremos perceber que a marca vermelha irá percorrer um círculo e, assim sendo, a distância entre a marca vermelha e o eixo do relógio será sempre a mesma, porém, a marca vermelha estará em movimento.
Trajetória
Quando observamos o risco de fumaça deixado no céu pelos aviões da esquadrilha da fumaça, estamos observando o caminho percorrido por cada um deles, os quais numa linguagem física definem a Trajetória de cada um, como exibe a figura a seguir:

Com base na informação acima podemos definir trajetória:
Ao conjunto das posições ocupadas sucessivamente por uma partícula em relação a um dado referencial é definido como trajetória.
Obs.: A trajetória de um corpo em movimento também depende do referencial adotado.
Vejamos dois exemplos para ilustrar a definição de trajetória:
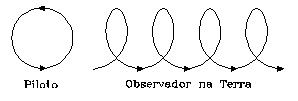
01 – O famoso e “temido” Barão Vermelho está em seu avião voando na horizontal, em linha reta e com velocidade constante.

Suponhamos que na extremidade da hélice exista uma marca de tinta a qual o piloto consiga ver enquanto a mesma gira.
Para o piloto, o movimento será circular (trajetória circular), enquanto que, para um observador em repouso na Terra, o movimento será helicoidal (trajetória helicoidal), como exibidas na figura a seguir:
02 – Um helicóptero se movimenta em linha reta na horizontal com velocidade constante e, em certo momento, um tripulante do helicóptero solta um sino que cai em direção à Terra, como mostra a figura a seguir.
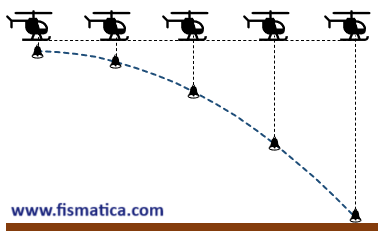
Desprezando a resistência do ar, quanto as trajetórias do sino, temos que:
- Para o observador que soltou o sino, a trajetória será uma linha reta (trajetória retilínea).
Ele verá o sino se afastando dele, pois, como não há resistência do ar, o sino continuará se deslocando na horizontal com a mesma velocidade do helicóptero, enquanto se desloca na vertical. Na prática, o observador estará sempre “sobre” o sino.
- Para um observador em repouso no solo, a trajetória será uma parábola (trajetória parabólica).
Ele verá o sino se deslocando na horizontal com a mesma velocidade do helicóptero, porém, o observador também vê o sino se deslocando na vertical.
Espaço (s)
Quando descrevemos uma trajetória precisamos de um sistema de referência espacial, ou seja, necessitamos de uma origem e uma orientação para podermos defini-la.
Espaço é uma grandeza física e tem como função expressar a posição de uma partícula em cada instante durante sua trajetória.
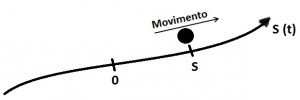
Obs.: na figura, a posição está representada em função do tempo s(t).
Unidades de espaço
No SI (Sistema Internacional de Medidas), a unidade de espaço é o metro (m), porém existem muitas outras unidades conhecidas como alguns múltiplos e submúltiplos do metro (km, cm, mm), ou ainda outras unidades como légua, milha, jarda, polegada, etc.
Deslocamento
Quando um móvel se desloca de uma posição A até uma posição B, calculamos seu deslocamento fazendo a diferença entre suas posições final e inicial.
Em linguagem matemática temos:
Onde:
representa a variação dos espaços
representa a posição final
representa a posição inicial
Obs.: como é comum em Física, a letra sem índice representa o estado final e a letra com um índice zero representa o estado inicial. No caso do deslocamento temos:
Note que quando partimos de uma determinada posição, percorremos uma trajetória qualquer e retornamos a posição inicial, o deslocamento será nulo.
Portanto, necessitamos de uma grandeza que meça o quanto percorremos de espaço durante um dado deslocamento.
Podemos definir então o espaço percorrido (ou distância percorrida) por um móvel como sendo a soma dos valores absolutos dos deslocamentos na ida e na volta, ou seja:
Tempo (t)
Tempo é uma noção primitiva (aceita sem definição) e fundamental na descrição de qualquer movimento.
Portanto não vamos definir tempo e sim trabalhar com suas variações, unidades e formas de medir.
A variação do tempo é dada pela expressão:
Unidades de tempo
No SI o tempo é medido em segundos (s). Outras unidades de tempo: hora (h), minuto (min), dia, ano, século, etc.
Sistemas de unidades
Podemos medir o tempo em pelo menos dois sistemas: o decimal e o sexagesimal. Nas equações horárias devemos utilizar o sistema decimal.
No sistema sexagesimal, temos:
1 h = 60 min
1 min = 60 s
1 h = 3.600 s
Obs.: Para passarmos do sistema decimal para o sexagesimal ou vice e versa, podemos utilizar uma regra de três.
Exercícios Resolvidos
01 – (FisMática) Um ciclista parte do km 20 de uma rodovia, se desloca até o km 90 e retorna a sua posição inicial. Determine:
a) Seu deslocamento;
b) O espaço percorrido pelo ciclista.
Resolução:
a) (como o ciclista retornou ao ponto de origem seu deslocamento é nulo)
b)
02 – (FisMática) Um soldado que está dentro de um bombardeiro, solta uma bomba para atingir seu alvo. Considerando que o avião permaneça voando em linha reta com velocidade constante e desprezando a resistência do ar que age sobre a bomba, determine o tipo de trajetória vista pelo soldado que soltou a bomba e por um observador que está parado em terra firme (no solo).
Soldado: como o avião permanece voando em linha reta com velocidade constante e desprezando a resistência do ar que age sobre a bomba, o soldado vai estar sempre “sobre a bomba”, vendo a mesma se deslocar em linha reta.
Observador no solo: ele vê a bomba se deslocando em duas dimensões, ou seja, há um movimento horizontal devido a velocidade que ela se solta do avião e o movimento de queda devido a força gravitacional. Portanto a trajetória vista pelo observador é uma parábola.
Exercícios Propostos
01 – Um caminhão que está fazendo entregas, parte do km 30 de uma rodovia e viaja até o km 270 onde descarrega uma parte da carga. Em seguida retorna até o km 50 onde termina de descarregar o restante. Determine:
a) seu deslocamento na ida;
b) seu deslocamento na volta;
c) seu deslocamento total;
d) a distância total percorrida.
02 – Um jovem está para num ponto de ônibus quando vê passar em sua frente uma carreta que se desloca com velocidade constante e em linha reta. Sobre a carroceria da carreta está um menino, parado em relação a mesma, quicando uma bola de basquete. Desprezando a resistência do ar, descreva a trajetória da bola de basquete vista:
a) pelo menino;
b) pelo jovem.
03 – (UNITAU-SP) Um móvel parte do km 50, indo até o km 60, de onde, mudando o sentido do movimento, vai até o km 32. A variação de espaço e a distância efetivamente percorrida são:
a) 28 km e 28 km
b) 18 km e 38 km
c) − 18 km e 38 km
d) − 18 km e 18 km
e) 38 km e 18 km
04 – (EFOA-MG) Um aluno, sentado na carteira da sala, observa os colegas, também sentados nas respectivas carteiras, bem como um mosquito que voa perseguindo o professor que fiscaliza a prova da turma. Das alternativas abaixo, a única que retrata uma análise correta do aluno é:
a) A velocidade de todos os meus colegas é nula para todo observador na superfície da Terra.
b) Eu estou em repouso em relação aos meus colegas, mas nós estamos em movimento em relação a todo observador na superfície da Terra.
c) Como não há repouso absoluto, não há nenhum referencial em relação ao qual nós, estudantes, estejamos em repouso.
d) A velocidade do mosquito é a mesma, tanto em relação ao meus colegas, quanto em relação ao professor.
e) Mesmo para o professor, que não pára de andar pela sala, seria possível achar um referencial em relação ao qual ele estivesse em repouso.
05 – Um homem está parado no degrau de uma escada rolante em movimento. Assinale a alternativa correta.
a) O movimento do homem e da escada são diferentes.
b) Para um referencial no solo, o homem não está em movimento.
c) Para um referencial na escada, o homem está em movimento.
d) Para um referencial no solo, a escada não está em movimento.
e) O homem está em repouso em relação a escada.
06 – (CEFET-PR) Imagine um ônibus escolar parado no ponto de ônibus e um aluno sentado em uma de suas poltronas. Quando o ônibus entra em movimento, sua posição no espaço se modifica: ele se afasta do ponto de ônibus. Dada esta situação, podemos afirmar que a conclusão ERRADA é que:
a) o aluno que está sentado na poltrona, acompanha o ônibus, portanto também se afasta do ponto de ônibus.
b) podemos dizer que um corpo está em movimento em relação a um referencial quando a sua posição muda em relação a esse referencial.
c) o aluno está parado em relação ao ônibus e em movimento em relação ao ponto de ônibus, se o referencial for o próprio ônibus.
d) neste exemplo, o referencial adotado é o ônibus.
e) para dizer se um corpo está parado ou em movimento, precisamos relacioná-lo a um ponto ou a um conjunto de pontos de referência.
07 – (UFSM – RS) Um avião voando em linha reta, com velocidade constante em relação ao solo, abandona uma bomba. Se a resistência do ar sobre ela puder ser desprezada, a trajetória dessa bomba será em forma de uma:
a) Parábola para um observador que estiver no avião;
b) Linha reta vertical para um observador que estiver na Terra;
c) Linha reta horizontal para um observador que estiver no avião;
d) Linha reta vertical para um observador que estiver no avião;
e) Mesma figura para qualquer observador, pois independe do referencial.
08 – (PUCSP) Leia com atenção a tira da Turma da Mônica mostrada abaixo e analise as afirmativas que se seguem, considerando os princípios da Mecânica Clássica.


I. Cascão encontra-se em movimento em relação ao skate e também em relação ao amigo Cebolinha.
II. Cascão encontra-se em repouso em relação ao skate, mas em movimento em relação ao amigo Cebolinha.
III. Em relação a um referencial fixo fora da Terra, Cascão jamais pode estar em repouso.
Estão corretas
a) apenas I b) I e II c) I e III d) II e III e) I, II e III
09 – Assinale a alternativa correta:
a) Deslocamento escalar e distância percorrida são conceitos iguais.
b) Se o espaço final de um corpo é igual ao espaço inicial dele, então podemos afirmar que ele ficou parado.
c) se o deslocamento escalar de um móvel é positivo, então podemos afirmar que ele se movimentou apenas a favor da orientação da trajetória.
d) Se o espaço final de um corpo é menor que o espaço inicial dele, então podemos afirmar que seu deslocamento escalar é negativo.
e) a distância percorrida por um corpo pode ser um número negativo.
10 – (UEPG-PR) Analise as proposições abaixo e marque cada uma delas com V (verdadeiro) ou F (falso):
a) ( ) O estudo da trajetória de uma partícula independe do referencial adotado.
b) ( ) Uma partícula que está em movimento em relação a um referencial pode estar em repouso em relação a outro.
c) ( ) Se dois móveis se deslocam por uma estrada retilínea com velocidades constantes e iguais, e no mesmo sentido, um está em repouso em relação ao outro.
A sequência correta obtida é:
a) F – V – F
b) F – F – V
c) V – F – V
d) V – V – F
e) F – V – V
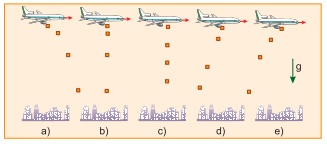
11 – (FUVEST) Em decorrência de fortes chuvas, uma cidade do interior paulista ficou isolada. Um avião sobrevoou a cidade, com velocidade horizontal constante, largando 4 pacotes de alimentos, em intervalos de tempos iguais. No caso ideal, em que a resistência do ar pode ser desprezada, a figura que melhor poderia representar as posições aproximadas do avião e dos pacotes, em um mesmo instante, é:
Gabarito
Ex. 01
a) Δsida= 240 km;
b) Δsvolta= – 220 km;
c) Δs = 20 km;
d) dp= 460 km.
Ex. 02
a) O menino vê um deslocamento em linha reta na direção vertical, ou seja, ele observa a bola descendo e subindo.
b) O jovem observa a trajetória da figura abaixo:
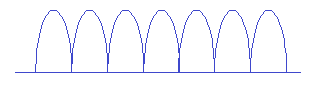
Ex. 03 – alternativa c.
Ex. 04 – alternativa e.
Ex. 05 – alternativa e.
Ex. 06 – alternativa d.
Ex. 07 – alternativa d.
Ex. 08 – alternativa d.
Ex. 09 – alternativa e.
Ex. 10 – alternativa d.