F3_DG_Aula 05 – Campo Elétrico: Aplicações
Campo Elétrico de várias Cargas Elétricas Puntiformes
Num sistema contendo várias cargas elétricas puntiformes, elas interagem entre si, porém como vimos na teoria, o campo elétrico é produzido por cada uma das cargas individualmente.
Para calcularmos o valor do campo elétrico em um ponto específico, podemos calcular o campo produzido por cada uma das cargas individualmente e determinarmos vetorialmente o Campo Elétrico Resultante.
Resumindo: num sistema isolado contendo cargas elétrica puntiformes Q1, Q2, Q3, …, Qn que produzem respectivamente num ponto P, em módulo, os campos elétricos E1, E2, E3, …, En , o vetor campo elétrico resultante será expressado por:
A seguir serão mostrados quatro tipos diferentes de aplicações utilizando duas cargas elétricas puntiformes com o objetivo de elucidar o assunto.
Obs.: no caso de se ter mais de duas cargas, o princípio de resolução será o mesmo.
01 – (FisMática) Considere duas cargas elétricas positivas, QA = 5 μC e QB = 8 μC. Determine o campo elétrico resultante no ponto P para cada um dos esquemas (sem escala) representados abaixo, levando em consideração que o meio seja “vácuo”.
Obs.: para ganharmos tempo, será calculado detalhadamente apenas o módulo de um dos campos elétricos. Para os outros serão apresentados apenas os resultados.
Lembretes:
01 – A unidades devem estar no SI, ou seja, a distância dever estar em metros;
02 – Por se tratar de vácuo, o valor da constante dielétrica será: k = 9.109 N.m2/C2;
03 – Transformação de unidade: 1 μC = 1.10-6 C.
a) Campo elétrico resultante em um ponto intermediário alinhado com as duas cargas.
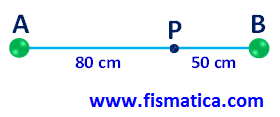
Cálculo do campo EA: QA = 5 μC e dAP = 80 cm = 0,8 m
Obs.: 103 N = 1 kN
Cálculo do campo EB: QB = 8 μC e dBP = 50 cm = 0,5 m
EB = 288,0 kN/C
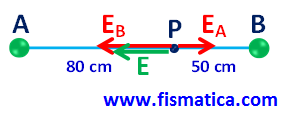
Campo Elétrico Resultante: como EA e EB tem a mesma direção e sentidos opostos, subtraímos os módulos, sendo que o vetor resultante terá a direção e sentido do vetor com maior módulo: EB.
(na dúvida sobre operações entre vetores veja: Cinemática Vetorial – Aula 02)
Módulo: E = EB – EA = 288,0 – 70,3 =>
Direção e sentido: representados no esquema abaixo.
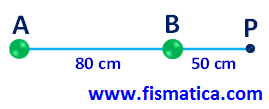
Cálculo do campo EA: QA = 5 μC e dAP = (80 +50) cm = 130 cm = 1,30 m
Cálculo do campo EB: QB = 8 μC e dBP = 50 cm = 0,5 m
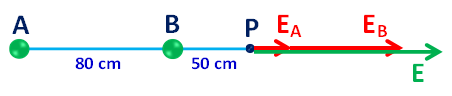
Campo Elétrico Resultante: como EA e EB tem a mesma direção e sentido, somamos os módulos, sendo que o vetor resultante também terá a mesma direção e sentido.
Módulo: E = EA + EB = 26,6 + 288,0 =>
Direção e sentido: representados no esquema abaixo.
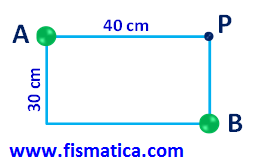
Cálculo do campo EA: QA = 5 μC e dAP = 40 cm = 0,40 m
Cálculo do campo EB: QB = 8 μC e dBP = 30 cm = 0,3 m
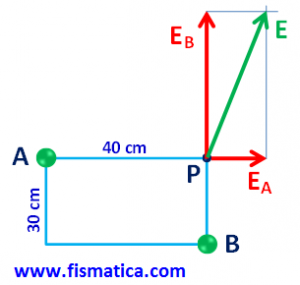
Campo Elétrico Resultante: como EA e EB tem direções e sentidos perpendiculares (a 90°), utilizamos o teorema de Pitágoras para calcularmos o módulo.
Módulo:
Direção e sentido: representados no esquema abaixo.
d) Campo elétrico resultante em um dos vértices de um Triângulo Equilátero, sendo que as cargas QA e QB estão posicionadas nos outros dois vértices como mostra o esquema abaixo.
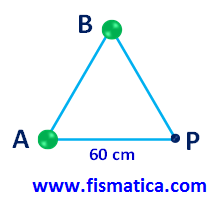
Cálculo do campo EA: QA = 5 μC e dAP = 60 cm = 0,60 m
Cálculo do campo EB: QB = 8 μC e dBP = 60 cm = 0,60 m
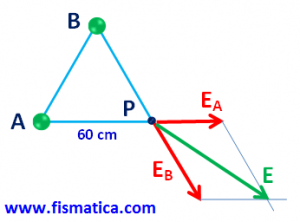
Campo Elétrico Resultante: como EA e EB tem direções e sentidos formando um ângulo de 60° utilizamos a lei dos cossenos para calcularmos o módulo. (os ângulos internos de um triângulo equilátero são iguais a 60°)
Módulo: (lembrete: cos 60° = 0,5)
Direção e sentido: representados no esquema abaixo.
Exercícios Propostos
01 – (UEG-GO) A figura a seguir representa as linhas de campo elétrico de duas cargas puntiformes.
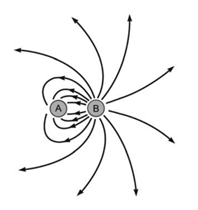
Com base na análise da figura, responda aos itens a seguir.
a) Quais são os sinais das cargas A e B? Justifique.
b) Crie uma relação entre os módulos das cargas A e B. Justifique.
c) Seria possível às linhas de campo elétrico se cruzarem? Justifique.
02 – (PUC-MG) As linhas de força de um campo elétrico são um modo conveniente de visualizar o campo elétrico e indicam a direção do campo em qualquer ponto. Leia as opções abaixo e assinale a afirmativa INCORRETA.
a) O número de linhas que saem ou que entram numa carga puntiforme é proporcional ao valor da carga elétrica.
b) As linhas de força saem da carga negativa e entram na carga positiva.
c) As linhas de força saem da carga positiva e entram na carga negativa.
d) O número de linhas por unidade de área perpendicular às linhas é proporcional à intensidade do campo.
03 – (UFV-MG) A figura a seguir representa a configuração de linhas de campo elétrico produzida por três cargas pontuais, todas com o mesmo módulo Q. Os sinais das cargas A, B e C são, respectivamente:
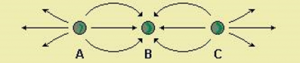
a) negativo, positivo e negativo.
b) negativo, negativo e positivo.
c) positivo, positivo e positivo.
d) negativo, negativo e negativo.
e) positivo, negativo e positivo.
04 – (UFF-RJ) Estão representadas, a seguir, as linhas de força do campo elétrico criado por um dipolo.
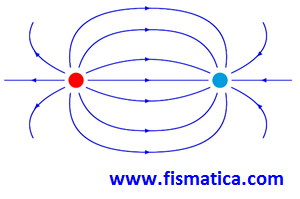
Considerando-se o dipolo, afirma-se:
I. A representação das linhas de campo elétrico resulta da superposição dos campos criados pelas cargas puntiformes.
II. O dipolo é composto por duas cargas de mesma intensidade e sinais contrários.
III. O campo elétrico criado por uma das cargas modifica o campo elétrico criado pela outra.
Com relação a estas afirmativas, conclui-se que:
a) apenas a I é correta.
b) apenas a II é correta.
c) apenas a III é correta.
d) apenas a I e a II são corretas.
e) apenas a II e a III são corretas.
05 – (MACK-SP) As cargas puntiformes q1 = 20 μC e q2 = 64 mC estão fixas no vácuo (k0 = 9×109 N.m2/C2), respectivamente nos pontos A e B.
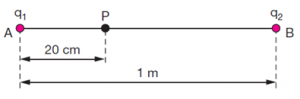
O campo elétrico resultante no ponto P tem intensidade de:
a) 3,0×106 N/C
b) 3,6×106 N/C
c) 4,0×106 N/C
d) 4,5×106 N/C
e) 5,4×106 N/C
06 – (PUC-PR) As linhas de força foram idealizadas pelo físico inglês Michael Faraday com o objetivo de visualizar o campo elétrico numa região do espaço. Em cada ponto de uma linha de força, a direção do campo elétrico é tangente à linha. Qual das afirmações abaixo NÃO cor responde a uma propriedade das linhas de força?
a) As linhas de força de um campo elétrico uniforme são paralelas e equidistantes entre si.
b) Para uma carga puntiforme positiva, as linhas de força apontam “para fora” da carga.
c) As linhas de força “convergem” para cargas puntiformes negativas.
d) Nas vizinhanças da superfície de um condutor isolado e carregado, as linhas de força são perpendiculares à superfície.
e) As linhas de força do campo elétrico são sempre fechadas.
07 – (UERJ) Duas cargas pontuais –q e +Q estão dispostas como ilustra a figura.

Se |+Q| > |– q|, o campo elétrico produzido por essas cargas se anula em um ponto situado:
a) à direita da carga positiva
b) à esquerda da carga negativa
c) entre as duas cargas e mais próximo da carga positiva
d) entre as duas cargas e mais próximo da carga negativa
08 – (PUC-MG) A figura mostra duas cargas de mesmo módulo e sinais opostos, colocadas a uma distância 2a, formando o que chamamos dipolo elétrico.
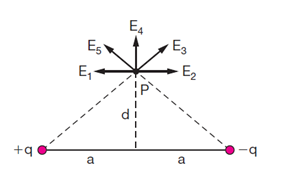
O vetor que representa corretamente o campo elétrico resultante E, produzido por essas cargas num ponto P, a uma distância d, é:
a) E1 b) E2 c) E3 d) E4 e) E5
09 – (PUCC-SP) Duas cargas puntiformes Q1 = –3,0×10-6 C e Q2 = +7,5×10-5 C estão fixas sobre um eixo x, nos pontos de abscissas 24 cm e 60 cm, respectivamente. Os módulos dos vetores campo elétrico gerados por Q1 e Q2 serão iguais nos pontos do eixo x cujas abscissas, em cm, valem:
a) -1 e 9,0
b) 9,0 e 15
c) 15 e 30
d) 30 e 36
e) 36 e 51
10 – (MACK-SP) O módulo do vetor campo elétrico (E) gerado por uma esfera metálica de dimensões desprezíveis, eletrizada positivamente, no vácuo (k0 = 9×109 N.m2/C2), varia com a distância ao seu centro (d), segundo o diagrama dado.
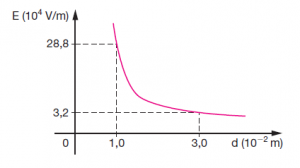
Sendo e = 1,6×10-19 C (módulo da carga do elétron ou do próton) a carga elementar, podemos afirmar que essa esfera possui:
a) um excesso de 1×1010 elétrons em relação ao número de prótons
b) um excesso de 2×1010 elétrons em relação ao número de prótons
c) um excesso de 1×1010 prótons em relação ao número de elétrons
d) um excesso de 2×1010 prótons em relação ao número de elétrons
e) igual número de elétrons e prótons
Gabarito
Ex. 01
a) Cargas positivas são fontes de campo elétrico enquanto cargas negativas são sorvedouros. Pela análise da figura, como as linhas de campo elétrico saem de B e chegam em A, conclui-se que a carga elétrica de A seja negativa e a de B positiva.
b) Da figura, percebemos que da carga B saem o dobro de linhas de campo que chegam na carga A, portanto: |QA| = 2|QB|.
c) Não. Pois caso fosse possível, haveria diferentes vetores campos elétricos em cada ponto de cruzamento das linhas de campo.
Ex. 02 – alternativa b.
Ex. 03 – alternativa e.
Ex. 04 – alternativa d.
Ex. 05 – alternativa b.
Ex. 06 – alternativa e.
Ex. 07 – alternativa b.
Ex. 08 – alternativa b.
Ex. 09 – alternativa c.
Ex. 10 – alternativa d.
