M1_DG_Aula 03 – Relações
Antes de entrarmos diretamente no conceito de Relação, vamos definir Par Ordenado e Produto Cartesiano
Par Ordenado
O conceito de Par Ordenado é primitivo, ou seja, não requer explicação ou definição.
Como o próprio nome diz, o Par Ordenado representa um Par de Símbolos Matemáticos, que podem ou não ser numéricos.
De uma forma genérica, podemos representar um par ordenado por (a, b), por exemplo, sendo que a ordem de posicionamento dos dois elementos importa, ou seja:
O nosso interesse nos pares ordenados consiste em definir os sistemas de coordenadas, como veremos a seguir.
Produto Cartesiano
“Dados dois conjuntos A e B, entende-se por Produto Cartesiano de A por B (AxB), ao conjunto formado por todos os pares ordenados possíveis, onde o primeiro elemento pertence ao conjunto A e o segundo ao conjunto B.”
Exemplo:
Dados os conjuntos A = {2, 4} e B = { 1, 3, 7}, o produto cartesiano de A por B é dado por:
AxB = {(2, 1); (2, 3); (2, 7); (4, 1); (4, 3); (4, 7)}
Definição Formal:
“Definidos dois conjuntos A e B, não vazios, o Produto Cartesiano de A por B é o conjunto de todos os Pares Ordenados obtidos sendo o primeiro elemento pertencente ao conjunto A e o segundo ao conjunto B.”
Representação matemática: AxB (A cartesiano B)
Plano Cartesiano
O Plano Cartesiano consiste em um sistema de coordenadas composto por dois eixos perpendiculares entre si.
O nome Plano Cartesiano se deve em homenagem ao filósofo René Descartes (1596 – 1650), que pela primeira vez utilizou o sistema para definir a localização de pontos no espaço.
Em Matemática, a forma mais conhecida do Plano Cartesiano, consiste em utilizar dois eixos, um horizontal (eixo x) e outro vertical (eixo y), tendo em comum o ponto zero, que é a origem do sistema, como mostra a figura a seguir:
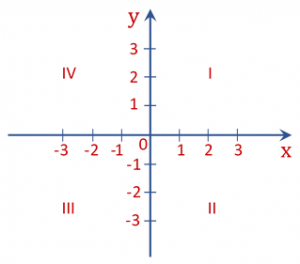
Obs.: Os números em romano I, II, III e IV representam os quadrantes do Plano Cartesiano.
Nomenclatura utilizada na matemática:
- (x, y) => coordenadas
- x => abcissa
- y => ordenada
Nota: propriedades dos quadrantes:
- Quadrante I: x > 0 e y > 0
- Quadrante II: x > 0 e y < 0
- Quadrante III: x < 0 e y < 0
- Quadrante IV: x < 0 e y > 0
Representação Gráfica
Considerando A e B, subconjuntos do conjunto dos números reais , a cada par ordenado (x, y) de números reais, pertencentes a AxB, associamos um ponto do Plano Cartesiano com abscissa x e ordenada y.
Obs.: o par ordenado (x, y) representa as coordenadas de um ponto qualquer do plano cartesiano.
Assim sendo, representar graficamente o produto cartesiano AxB, nada mais é do que representar num plano todos os pontos associados aos elementos de AxB.
Exemplo:
Dados A = {2, 5} e B = {1, 4}, temos que AxB = {(2, 1); (2, 4); (5, 1); (5, 4)}, sendo sua representação gráfica dada pela figura a seguir:
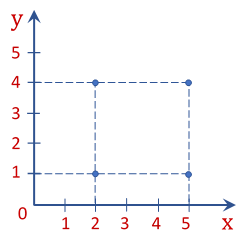
Relações
Sejam dois conjuntos A e B e o conjunto formado por AxB.
Podemos obter vários subconjuntos de AxB, de forma aleatória ou utilizando uma determinada Relação entre seus elementos.
Definição:
“Dados dois conjuntos A e B, definimos o conjunto R (relação), subconjunto de AxB, cujos elementos obedecem a uma regra que relaciona os elementos de A com os de B.”
Exemplo:
Sejam os conjuntos A = {2, 3, 4, 5} e B = {0, 1, 3}, sendo o produto cartesiano dado por:
AxB = {(2, 0); (2, 1); (2, 3); (3, 0); (3, 1); (3, 3); (4, 0); (4, 1); (4, 3); (5, 0); (5, 1); (5, 3)}
Determine o conjunto R, de pares ordenados (x, y), sendo definida a Relação: y = x – 2.
Resolução:
Para cada elemento do conjunto A (x), devemos subtrair duas unidades para obter cada elemento (y) pertencente ao conjunto B.
R = {(2, 0); (3, 1); (5, 3)}
Obs.: notem que nem todos elementos de AxB satisfazem a relação dada.
Diagrama de Flechas
Num Diagrama de Flechas, os conjuntos A e B são representados por duas “figuras geométricas” que contém os elementos de cada conjunto.
Dada uma relação R, são desenhadas “flechas” que partem de A e chegam em B, representando a regra da relação.
Exemplo:
Sendo A = {0, 2, 4} e B = {0, 1, 3, 5}, represente a relação .
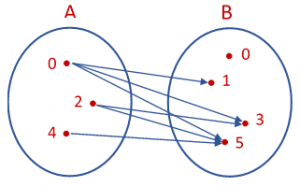
Domínio e Imagem
Para entendermos melhor os conceitos de Domínio e Imagem, vamos observar o exemplo a seguir:
Sejam os conjuntos A = {0, 1, 2, 3, 4, 5} e B = {0, 2, 4, 6, 8}.
Represente a relação R por um diagrama de flechas, sendo: .
Solução:
A cada elemento (a), pertencente ao conjunto A, vamos somar duas unidades para obter o elemento (b), pertencente ao conjunto B.
R = {(0, 2); (2, 4); (4, 6)}
Pelo diagrama de flechas, temos:
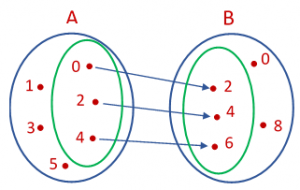
Podemos notar que os elementos que entraram na relação formaram dois subconjuntos, um de A e outro de B:
- O subconjunto contido em A, é denominado de Domínio da Relação
- O subconjunto contido em B, é denominado de Imagem da Relação
Na forma de conjuntos, temos que:
- D(R) = {0, 2, 4}
- Im(R) = {2, 4, 6}
Exercícios Resolvidos
01 – (UFRN) O jogo da velha tradicional consiste em um tabuleiro quadrado dividido em 9 partes, no qual dois jogadores, alternadamente, vão colocando peças (uma a cada jogada). Ganha o jogo aquele que alinhar, na horizontal, na vertical ou na diagonal, três de suas peças.
Uma versão chamada JOGO DA VELHA DE DESCARTES, em homenagem ao criador da geometria analítica, René Descartes, consiste na construção de um subconjunto do plano cartesiano, no qual cada jogador, alternadamente, anota as coordenadas de um ponto do plano. Ganha o jogo aquele que primeiro alinhar três de seus pontos. A sequência abaixo é o registro da sequência das jogadas de uma partida entre dois jogadores iniciantes, em que um anotava suas jogadas com a cor preta e o outro, com a cor cinza. Eles desistiram da partida sem perceber que um deles havia ganhado.
((1,1), (2,3), (2,2), (3,3), (4,3), (1,3), (2,1), (3,1), (3,2), (4,2))
Com base nessas informações, é correto afirmar que o jogador que ganhou a partida foi o que anotava sua jogada com a cor
a) cinza, em sua terceira jogada.
b) preta, em sua terceira jogada.
c) cinza, em sua quarta jogada.
d) preta, em sua quarta jogada.
Resposta:
Considere a figura:
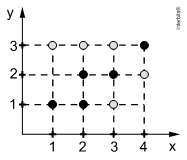
De acordo com a sequência de jogadas apresentada, podemos concluir que o jogador que ganhou a partida foi o que anotava sua jogada com a cor cinza, em sua terceira jogada, ou seja, na jogada (1,3). (alternativa a)
02 – (UFRN) Considerando K = {1, 2, 3, 4}, marque a opção cuja figura representa o produto cartesiano K × K.
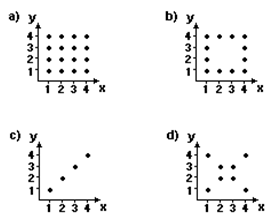
Resposta:
O conjunto dos pares ordenados do produto cartesiano K × K é:
((1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4))
Observando as figuras, vemos a resposta correta é a alternativa a.
Exercícios Propostos
01 – (ENEM) Alunos de um curso de engenharia desenvolveram um robô “anfíbio” que executa saltos somente nas direções norte, sul, leste e oeste. Um dos alunos representou a posição inicial desse robô, no plano cartesiano, pela letra P na ilustração.

A direção norte-sul é a mesma do eixo y, sendo que o sentido norte é o sentido de crescimento de y, e a direção leste-oeste é a mesma do eixo x, sendo que o sentido leste é o sentido de crescimento de x.
Em seguida, esse aluno deu os seguintes comandos de movimentação para o robô: 4 norte, 2 leste e 3 sul, nos quais os coeficientes numéricos representam o número de saltos do robô nas direções correspondentes, e cada salto corresponde a uma unidade do plano cartesiano.
Depois de realizar os comandos dados pelo aluno, a posição do robô, no plano cartesiano, será
a) (0; 2) b) (0; 3) c) (1; 2) d) (1; 4) e) (2; 1)
02 – (ENEM) Uma pesquisa do Instituto de Pesquisa Econômica (Ipea) investigou qual área faz a economia crescer mais e quais os maiores responsáveis pela diminuição da desigualdade na distribuição de renda.

Considerando apenas as áreas que contribuem para o crescimento econômico mais do que o investimento em exportação, qual delas é a que mais influência para a maior igualdade?
a) Bolsa família.
b) Educação.
c) Investimento em construção civil.
d) Previdência Social.
e) Saúde.
TEXTO PARA A PRÓXIMA QUESTÃO:
As atividades de comunicação humana são plurais e estão intimamente ligadas às suas necessidades de sobrevivência. O problema de contagem, por exemplo, se confunde com a própria história humana no decorrer dos tempos. Assim como para os índios mundurucus, do sul do Pará, os waimiri-atroari, contam somente de um até cinco, adotando os seguintes vocábulos: awynimi é o número 1, typytyna é o 2, takynima é o 3, takyninapa é o 4, e, finalmente, warenipa é o 5.
Texto Adaptado: Scientific American – Brasil, “Etnomatática”. Edição Especial, Nº 11, ISSN 1679-5229
03 – (UEPA) Considere A o conjunto formado pelos números utilizados no sistema de contagem dos waimiriatroari, ou seja, A = {1, 2, 3, 4, 5}. Nestas condições, o número de elementos da relação R1 = {(x, y) ∈ A×A/ y ≥ x} é igual a:
a) 5 b) 10 c) 15 d) 20 e) 25
TEXTO PARA A PRÓXIMA QUESTÃO:
Sistema de irrigação por Pivô Central

A divisão da área em piquetes tem sido realizada de formas diferentes. Algumas favorecem o manejo da pastagem e dos animais e outras favorecem o manejo da irrigação e da fertirrigação. É realmente difícil encontrar uma maneira que favoreça as duas situações. O que devemos fazer é analisarmos a situação e optarmos pela forma de dividir a área irrigada.
A mais utilizada é a forma de pizza, como segue na ilustração ao lado, pois dentre outras coisas, favorece em muito o processo de fertirrigação. A área de lazer pode ser feita no centro ou na periferia do Pivô.
Adap. de: DRUMOND, Luis C. D. Irrigação de pastagens – in: II Simpósio Internacional de Produção de Gado de Corte.
Disponível em: http://www.simcorte.com/index/Palestras/6_simcorte/simcorte12.pdf Acesso: 08 out. 2013
04 – (IFSC) Considerando que há 30 piquetes na ilustração da figura do texto, cada um deles é identificado com um número de 1 a 30 no sentido horário, o gado ocupa um único piquete por vez e é remanejado para o próximo piquete, em sentido horário a cada 2 meses, analise as seguintes afirmações feitas sobre a função que determina o número do piquete ocupado, em relação ao número de meses passados, após o início de funcionamento desse manejo.
I. O número do piquete ocupado é o domínio dessa função.
II. O número do mês é a imagem da função.
III. Essa é uma função periódica, sendo seu domínio igual a 60 meses.
É CORRETO afirmar que:
a) Apenas a afirmação III é verdadeira.
b) Apenas as afirmações I e II são verdadeiras.
c) Apenas as afirmações II e III são verdadeiras.
d) Apenas a afirmação I é verdadeira.
e) Todas as afirmações são verdadeiras.
05 – (UFV) Os pares ordenados (1,2), (2,6), (3,7), (4,8) e (1,9) pertencem ao produto cartesiano A×B. Sabendo-se que A×B tem 20 elementos, é correto afirmar que a soma dos elementos de A é:
a) 9 b) 11 c) 10 d) 12 e) 15
06 – (UNESP) Os habitantes de um planeta chamado Jumpspace locomovem-se saltando. Para isto, realizam apenas um número inteiro de saltos de dois tipos, o slow jump (SJ) e o quick jump (QJ). Ao executarem um SJ saltam sempre 20 u.d. (unidade de distância) para Leste e 30 u.d. para Norte. Já no QJ saltam sempre 40 u.d. para Oeste e 80 u.d. para Sul.
Um habitante desse planeta deseja chegar exatamente a um ponto situado 204 u.d. a Leste e 278 u.d. ao Norte de onde se encontra. Nesse caso, é correto afirmar que o habitante
a) conseguirá alcançar seu objetivo, realizando 13 saltos SJ e 7 QJ.
b) conseguirá alcançar seu objetivo, realizando 7 saltos SJ e 13 QJ.
c) conseguirá alcançar seu objetivo, realizando 13 saltos SJ.
d) não conseguirá alcançar seu objetivo, pois não há número inteiro de saltos que lhe permita isso.
e) conseguirá alcançar seu objetivo, realizando 7 saltos QJ.
07 – (UEPB) Os conjuntos A e B têm, respectivamente, 5 – x e 3x elementos e A×B tem 8x + 2 elementos. Então, se pode admitir como verdadeiro que:
a) A tem cinco elementos
b) B tem quatro elementos
c) B tem seis elementos
d) A tem mais de seis elementos
e) B tem menos de três elementos
08 – (CFTMG) Nos conjuntos P = {0, 1, 2} e R = {(x, y) ∈ P×P / x + y < 3}, o número de elementos do conjunto R é igual a
a) 3 b) 4 c) 5 d) 6
09 – (UFSM) Escolhendo aleatoriamente alguns números das páginas de um livro adquirido numa livraria, foram formados os conjuntos A = {2, 5, 6} e B = {1, 3, 4, 6, 8}, sendo a relação definida por R = {(x, y) ∈ A×B / x ≥ y}. Dessa forma,
a) D(R) = {2, 5, 6} e Im(R) = {1, 3, 4, 6, 8}
b) D(R) = {2, 5, 6} e Im(R) = {1, 3, 4, 6}
c) D(R) = {2,5} e Im(R) = {1, 3, 4, 6}
d) D(R) = {5,6} e Im(R) = {1, 3, 4, 6, 8}
e) D(R) = {2, 5, 6} e Im(R) = {4, 6, 8}
10 – (CFTMG) Sendo A um ponto de coordenadas (2x + 4, 3x – 9) do quarto quadrante do plano cartesiano, é correto afirmar que x pertence ao intervalo real
a) – 2 < x < 3 b) 2 ≤ x ≤ 3 c) – 3 < x < 2 d) – 3 ≤ x ≤ 2
Gabarito
Ex. 01 – alternativa c.
Ex. 02 – alternativa e.
Ex. 03 – alternativa c.
Ex. 04 – alternativa a.
Ex. 05 – alternativa c.
Ex. 06 – alternativa d.
Ex. 07 – alternativa c.
Ex. 08 – alternativa c.
Ex. 09 – alternativa b.
Ex. 10 – alternativa a.
