M2_Aula 03 – PA: Propriedades e Soma

Propriedades de uma PA

Inicialmente vamos entender as propriedades de uma PA verificando diretamente em dois exemplos práticos, para depois chegarmos a uma expressão que represente tais propriedades.

1 – Consideremos a PA com primeiro termo igual a 2 e razão 3:

PA = (2, 5, 8, 11, 14. 17, 20, 23, …)

Vamos utilizar um termo qualquer e calcular a média aritmética (MA) entre o seu antecessor e seu sucessor:

Termo 11: MA₁₁ = (8 + 14)/2 = 22/2 => MA₁₁ = 11
Termo 17: MA₁₇ = (14 + 20)/2 = 34/2 => MA₁₇ = 17

Que interessante!!! A média aritmética é igual ao próprio termo!!

Vamos ver mais um exemplo.

2 – Consideremos a PA com primeiro termo igual a 5 e razão 6:

PA = (5, 11, 17, 23, 29. 35, 41, 47, …)

Vamos utilizar um termo qualquer e calcular a média aritmética (MA) entre o seu antecessor e seu sucessor:

Termo 23: MA₂₃ = (17 + 29)/2 = 46/2 => MA₂₃ = 23
Termo 41: MA₄₁ = (35 + 47)/2 = 82/2 => MA₄₁ = 41

Novamente, a média aritmética é igual ao próprio termo.

Bom, isso não é coincidência e sim uma propriedade das PAs.

Baseado nos dois exemplos anteriores, vamos generalizar a propriedade.

Sejam um termo genérico a_p, seu antecessor a_p-1 e seu sucessor a_p+1.

A PA genérica, seria dada por:

PA = (a₁, a₂, a₃, …, a_p-1, a_p, a_p+1, …, a_n, …)

Propriedade:

“Numa PA, com exceção dos extremos, um termo qualquer sempre será igual a média aritmética entre seu antecessor e seu sucessor.”

Em forma de expressão matemática, temos que:

$\dpi{100} \mathbf{a_{p}=\frac{a_{p-1}+a_{p+1}}{2}}$

Vamos agora ver uma segunda propriedade das PAs finitas, utilizando para tanto um exemplo, como fizemos anteriormente.

Consideremos a PA finita com 12 termos, sendo o primeiro termo igual a 2 e razão 3:

PA = (2, 5, 8, 11, 14. 17, 20, 23, 26, 29, 32, 35)

Vamos somar dois termos de forma que a “distância” do primeiro ao primeiro termo seja igual a do segundo em relação ao último termo.

Exemplos:

5 + 32 = 37
8 + 29 = 37
11 + 26 = 37

Agora vamos somar os extremos: 2 + 35 = 37

Vejam que interessante!!! A soma dos termos equidistantes do primeiro e último é uma constante e igual à soma dos extremos!!!

Baseado no exemplo anterior, vamos generalizar a propriedade.

A PA genérica, seria dada por:

PA = (a₁, a₂, a₃, …, a_1+p, …, a_{n – p}, …, a_n-2, a_n-1, a_n)

Propriedade:

“Numa PA finita, a soma de dois termos equidistantes dos extremos sempre será igual a própria soma dos extremos.”

Em forma de expressão matemática, temos que:

$\dpi{100} \mathbf{a_{1}+a_{n}=a_{p+1}+a_{n-p}}$

Soma dos termos de uma PA finita

Desde meu ensino médio, lembro quando ouvi pela primeira vez a façanha de um professor de matemática que não estava muito a fim de dar aula e passou para seus alunos a tarefa de somar os números de 1 a 100.

O problema é que na sala de aula estava um aluno de 9 anos, chamado Gauss (Johann Carl Friedrich Gauss, 1777 – 1855), que fez a conta em poucos segundos.

Para espanto do professor o resultado apresentado por Gauss estava certo!!!

Vamos ver como foi que Gauss pensou.

Seja a soma a ser realizada na ordem crescente e decrescente:

S = 1 + 2 + 3 + 4 + … + 97 + 98 + 99 + 100

S = 100 + 99 + 98 + 97 + … + 4 + 3 + 2 + 1

Gauss observou que quando se somavam os termos equivalentes, se obtinha um valor fixo:

Exemplos:

1 + 100 = 101
2 + 99 = 101
3 + 98 = 101

E assim sucessivamente.

Somando os lados antes e depois da igualdade, temos que:

S + S = 101 + 101 + 101 + … (100 vezes)

2S = 101×100 => s = 10100/2 => S = 5.050

Fantástico, não!!!

Baseado no raciocínio de Gauss, também podemos pensar da seguinte forma:

Observando a figura, vemos que, como estamos somando os termos de dois em dois, teremos 50 somas de 101, ou seja:

S = 50×101 => S = 5.050

Que é o mesmo resultado obtido anteriormente.

Utilizando o último raciocínio, podemos chegar a uma expressão geral para a soma dos n termos de uma PA finita:

$\dpi{100} \mathbf{S_{n}=\frac{\left ( a_{1}+a_{n} \right ).n}{2}}$

Exercícios Resolvidos

01 – (FUVEST) O cilindro de papelão central de uma fita crepe tem raio externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100 voltas completas.

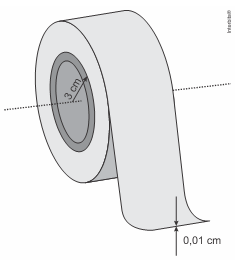
Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, o comprimento total da fita é de, aproximadamente, (Note e adote: π ≌ 3,14)

a) 9,4 m b) 11,0 m c) 18,8 m d) 22,0 m e) 25,1 m

Resolução:

Lembrete: comprimento de um círculo => c = 2.π.r

Espessura da fita: e = 0,01 cm

Acréscimo do raio em cada volta: r_p+1= r_p + e => r_p+1= r_p + 0,01

Os raios aumentam segundo a PA finita:

Com 100 voltas: n = 100

Primeiro termo: a₁ = 3,01

Razão: r = 0,01

Último termo: a₁₀₀ = a₁ + 99.r = 3,01 + 99×0,01 => a₁₀₀ = 4,00

PA = (3,00, 3,01, 3,02, 3,03, 3,04, …, 4,00)

O comprimento total da fita será igual a C = 2.π.S₁₀₀

C = 2.π.3,00 + 2.π.3,01 + 2.π.3,02 + … + 2.π.4,00 => C = 2.π.S₁₀₀

Cálculo da soma da PA:

$\dpi{100} S_{n}=\frac{\left ( a_{1}+a_{n} \right ).n}{2}\Rightarrow S_{100}=\frac{\left ( 3,01+4,00 \right ).100}{2}=350,5$

Finalmente o cálculo do comprimento total:

C = 2.π.S₁₀₀ = 2×3,14×350,5 => C = 2201,14 cm (alternativa d)

02 – (UPF) De uma progressão aritmética a_n de razão r, sabe-se que a₈ = 16 e a₁₄ = 4. Seja S_n a soma dos n primeiros termos de a_n, o menor valor de n, de modo que S_n = 220, é

a) 12 b) 11 c) 14 d) 16 e) 18

Resolução:

Primeiramente vamos determinar o primeiro termo a₁ e a razão r da PA.

a₈ = a₁ + 7.r => 16 = a₁ + 7.r ( eq. I )

a₁₄ = a₁ + 13.r => 4 = a₁ + 13.r ( eq. II )

Isolando o termo a₁ da (eq. I) e substituindo na (eq. II), temos:

(eq. I) a₁ = 16 – 7.r

(eq. II) 4 = a₁ + 13.r => 4 = (16 – 7.r) + 13.r => 4 – 16 = – 7.r + 13.r => – 12 = 6.r => r = – 2

Substituindo o valor de r na (eq. I), temos:

a₁ = 16 – 7.r = 16 – 7x(– 2) = 16 + 14 => a₁ = 30

Seguindo o enunciado, vamos calcular n para que tenhamos S_n = 220.

$\dpi{100} S_{n}=\frac{\left ( a_{1}+a_{n} \right ).n}{2}\Rightarrow 220=\frac{\left \{ a_{1}+ \left [ a_{1}+\left ( n-1 \right ) \right ].r\right \}.n}{2}$

2×220 = (30 + 30 – 2.n + 2).n => 440 = 62.n – 2.n²

Simplificando por 2 e rearranjando os termos, temos uma equação do 2º grau em n:

n² – 31.n + 220 = 0

Soluções da equação:

$\dpi{100} n=\frac{-b\pm \sqrt{b^{2}-4.a.c}}{2.a}=\frac{-\left ( -31 \right )\pm \sqrt{\left (-31 \right )^{2}-4\times 1\times 220}}{2\times 1}$

$\dpi{100} n=\frac{31 \pm \sqrt{961-880}}{2}=\frac{31 \pm \sqrt{81}}{2}=\frac{31\pm 9}{2}$

Soluções:

n₁ = (31 + 9)/2 => n₁ = 20
n₂ = (31 – 9)/2 => n₂ = 11

Menor valor de n: n = 11 (alternativa b)

Exercícios Propostos

01 – (UNICAMP) Considere que (a, b, 3, c) é uma progressão aritmética de números reais, e que a soma de seus elementos é igual a 8. O produto dos elementos dessa progressão é igual a

a) 30 b) 10 c) – 15 d) – 20

02 – (ESCOLA NAVAL) Seja S_n = n² + n + 1 a soma dos termos de uma sequência numérica Sobre essa sequência assinale a opção correta.

a) Essa sequência numérica não é uma progressão aritmética.

b) A diferença entre o quinto e o quarto termo é 3.

c) Sua razão é 4.

d) S_n é um número múltiplo de 7.

e) Seu sétimo termo é 32.

03 – (ENEM) Um hotel de 3 andares está sendo construído. Cada andar terá 100 quartos. Os quartos serão numerados de 100 a 399 e cada um terá seu número afixado à porta. Cada número será composto por peças individuais, cada uma simbolizando um único algarismo.

Qual a quantidade mínima de peças, simbolizando o algarismo 2, necessárias para identificar o número de todos os quartos?

a) 160 b) 157 c) 130 d) 120 e) 60

04 – (UECE) A listagem infinita de números naturais apresentada abaixo está organizada e ordenada segundo uma lógica estrutural própria:

1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1, 2, 3, …

O resultado da soma dos primeiros 2020 números da listagem apresentada é

a) 7007 b) 7700 c) 7070 d) 7770

05 – (UDESC) Sejam $\dpi{100} \left ( 16,\, 18,\, 20,\, \cdots \right )$ e $\dpi{100} \left ( \frac{1}{2},\, 3,\, \frac{11}{2},\, \cdots \right )$ duas progressões aritméticas. Estas duas progressões apresentarão somas iguais, para uma mesma quantidade de termos somados, quando o valor da soma for igual a:

a) 154 b) 4.774 c) 63 d) 4.914 e) 1.584

06 – (UEFS) Uma progressão aritmética (PA) possui 17 termos, todos positivos. A diferença entre o maior termo (a₁₇) e o menor termo (a₁) dessa PA é igual a 48. Sabendo que, dentre os números primos que ocorrem nessa PA, 13 é o menor e 43 é o maior, o valor de a₁ + a₁₇ é

a) 59 b) 62 c) 65 d) 68 e) 71

07 – (AMAN) Uma fábrica de tratores agrícolas, que começou a produzir em 2010, estabeleceu como meta produzir 20.000 tratores até o final do ano de 2025. O gráfico abaixo mostra as quantidades de tratores produzidos no período 2010-2017.

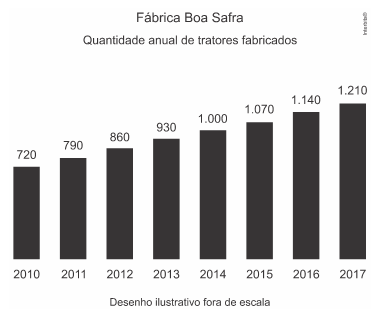
Admitindo que a quantidade de tratores produzidos evolua nos anos seguintes segundo a mesma razão de crescimento do período 2010-2017, é possível concluir que a meta prevista

a) deverá ser atingida, sendo superada em 80 tratores.

b) deverá ser atingida, sendo superada em 150 tratores.

c) não deverá ser atingida, pois serão produzidos 1.850 tratores a menos.

d) não deverá ser atingida, pois serão produzidos 150 tratores a menos.

e) não deverá ser atingida, pois serão produzidos 80 tratores a menos.

08 – (ACAFE) Sendo X_n a soma dos n primeiros termos da sequência (3, 5, 7, 9, 11, …) e Y_n o n-ésimo termo da sequência (-3, -35, -67, -99, …) então, a soma dos valores de n sabendo que X_n = Y_n e igual a:

a) 32 b) 34 c) 29 d) 30

09 – (UECE) Seja (a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈) uma progressão aritmética. Se a₂ + a₅ = 8 e a₈ = 7, então a₃ + a₇ é igual a:

a) 8 b) 28/3 c) 10 d) 32/3

10 – (MACK) Numa sequência aritmética de 17 termos, sabe-se que A₅ = 3 e A₁₃ = 7. Então a soma de todos os termos é:

a) 102 b) 85 c) 68 d) 78 e) 90

11 – (ENEM) Em uma corrida de regularidade, cada corredor recebe um mapa com o trajeto a ser seguido e uma tabela indicando intervalos de tempo e distâncias entre postos de averiguação. O objetivo dos competidores é passar por cada um dos postos de averiguação o mais próximo possível do tempo estabelecido na tabela. Suponha que o tempo previsto para percorrer a distância entre dois postos de verificação consecutivos seja sempre de 5 min 15 s e que um corredor obteve os seguintes tempos nos quatro primeiros postos.

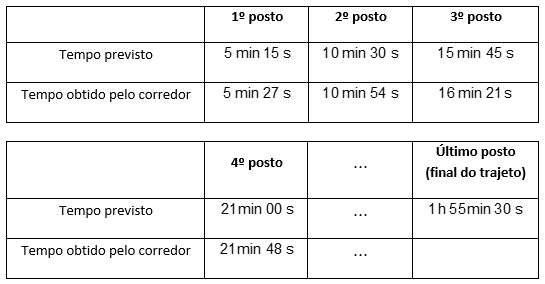
Caso esse corredor consiga manter o mesmo ritmo, seu tempo total de corrida será

a) 1 h 55 min 42 s

b) 1 h 56 min 30 s

c) 1 h 59 min 54 s

d) 2 h 05 min 09 s

e) 2 h 05 min 21 s

12 – (ESCOLA NAVAL) Quantos números inteiros entre 1 e 1.000 são divisíveis por 3 ou por 7?

a) 47 b) 142 c) 289 d) 333 e) 428

Gabarito

Ex. 01 – alternativa c.

Ex. 02 – alternativa a.

Ex. 03 – alternativa a.

Ex. 04 – alternativa c.

Ex. 05 – alternativa d.

Ex. 06 – alternativa d.

Ex. 07 – alternativa e.

Ex. 08 – alternativa d.

Ex. 09 – alternativa c.

Ex. 10 – alternativa b.

Ex. 11 – alternativa c.

Ex. 12 – alternativa e.

Deixe uma resposta Cancelar resposta

Você precisa fazer o login para publicar um comentário.

M2_Aula 03 – PA: Propriedades e Soma

Propriedades de uma PA

Soma dos termos de uma PA finita

Exercícios Resolvidos

Exercícios Propostos

Gabarito

Deixe uma resposta Cancelar resposta

Faça login com sua conta de site

Registre uma nova conta

Modal title